

新高考数学一轮复习讲义 第5章 §5.3 平面向量的数量积
展开课本上和老师讲解的例题,一般都具有一定的典型性和代表性。要认真研究,深刻理解,要透过“样板”,学会通过逻辑思维,灵活运用所学知识去分析问题和解决问题,特别是要学习分析问题的思路、解决问题的方法,并能总结出解题的规律。
2、精练习题
复习时不要搞“题海战术”,应在老师的指导下,选一些源于课本的变式题,或体现基本概念、基本方法的基本题,通过解题来提高思维能力和解题技巧,加深对所学知识的深入理解。在解题时,要独立思考,一题多思,一题多解,反复玩味,悟出道理。
3、加强审题的规范性
每每大考过后,总有同学抱怨没考好,纠其原因是考试时没有注意审题。审题决定了成功与否,不解决这个问题势必影响到高考的成败。那么怎么审题呢? 应找出题目中的已知条件 ;善于挖掘题目中的隐含条件 ;认真分析条件与目标的联系,确定解题思路 。
4、重视错题
“错误是最好的老师”,但更重要的是寻找错因,及时进行总结,三五个字,一两句话都行,言简意赅,切中要害,以利于吸取教训,力求相同的错误不犯第二次。
§5.3 平面向量的数量积
考试要求 1.理解平面向量数量积的含义及其物理意义.2.了解平面向量的数量积与投影向量的关系.3.掌握数量积的坐标表达式,会进行平面向量数量积的运算.4.能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系.5.会用向量的方法解决某些简单的平面几何问题.
知识梳理
1.向量的夹角
已知两个非零向量a,b,O是平面上的任意一点,作eq \(OA,\s\up6(→))=a,eq \(OB,\s\up6(→))=b,则∠AOB=θ(0≤θ≤π)叫做向量a与b的夹角.
2.平面向量的数量积
已知两个非零向量a与b,它们的夹角为θ,我们把数量|a||b|cs θ叫做向量a与b的数量积,记作a·b.
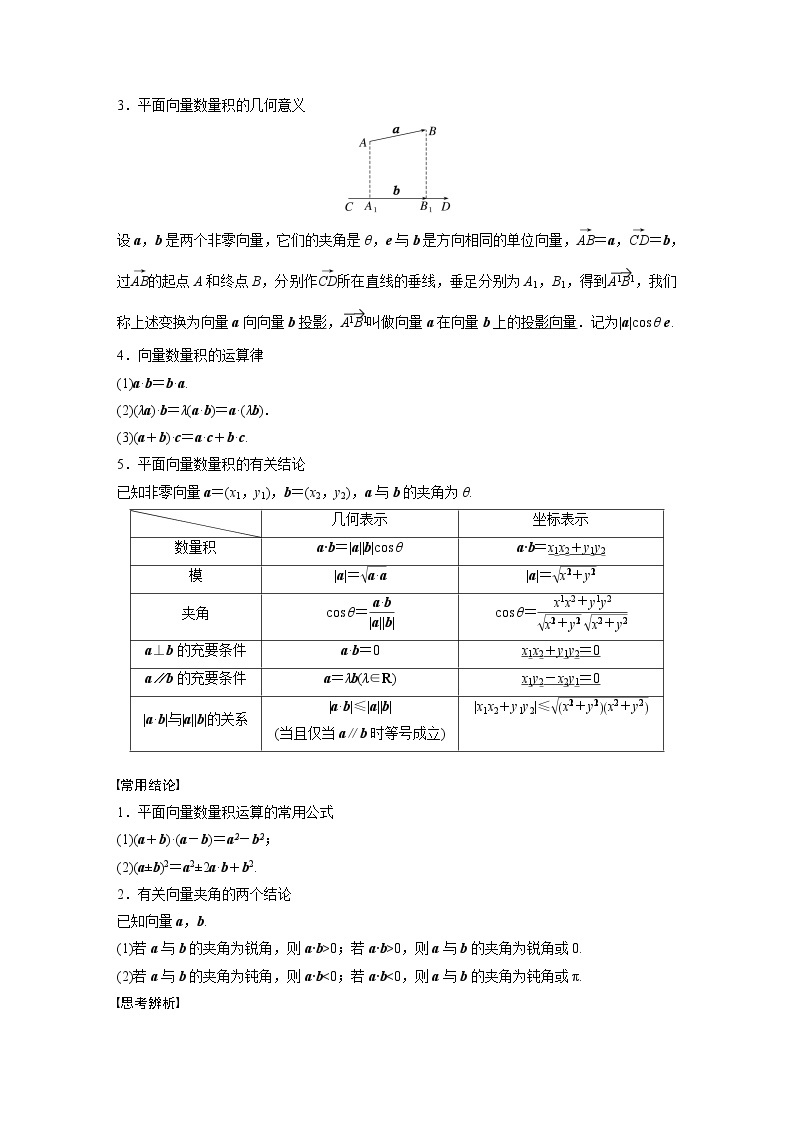
3.平面向量数量积的几何意义
设a,b是两个非零向量,它们的夹角是θ,e与b是方向相同的单位向量,eq \(AB,\s\up6(→))=a,eq \(CD,\s\up6(→))=b,过eq \(AB,\s\up6(→))的起点A和终点B,分别作eq \(CD,\s\up6(→))所在直线的垂线,垂足分别为A1,B1,得到eq \(A1B1,\s\up6(—→)),我们称上述变换为向量a向向量b投影,eq \(A1B1,\s\up6(—→))叫做向量a在向量b上的投影向量.记为|a|cs θ e.
4.向量数量积的运算律
(1)a·b=b·a.
(2)(λa)·b=λ(a·b)=a·(λb).
(3)(a+b)·c=a·c+b·c.
5.平面向量数量积的有关结论
已知非零向量a=(x1,y1),b=(x2,y2),a与b的夹角为θ.
常用结论
1.平面向量数量积运算的常用公式
(1)(a+b)·(a-b)=a2-b2;
(2)(a±b)2=a2±2a·b+b2.
2.有关向量夹角的两个结论
已知向量a,b.
(1)若a与b的夹角为锐角,则a·b>0;若a·b>0,则a与b的夹角为锐角或0.
(2)若a与b的夹角为钝角,则a·b<0;若a·b<0,则a与b的夹角为钝角或π.
思考辨析
判断下列结论是否正确(请在括号中打“√”或“×”)
(1)两个向量的夹角的范围是eq \b\lc\[\rc\](\a\vs4\al\c1(0,\f(π,2))).( × )
(2)若a·b>0,则a和b的夹角为锐角.( × )
(3)两个向量的数量积是一个实数,向量的加、减、数乘运算的结果是向量.( √ )
(4)(a·b)·c=a·(b·c).( × )
教材改编题
1.(多选)(2022·海南省临高二中模拟)设a,b,c是任意的非零向量,则下列结论正确的是( )
A.0·a=0
B.a·b=b·c,则a=c
C.a·b=0⇒a⊥b
D.(a+b)·(a-b)=|a|2-|b|2
答案 CD
2.已知向量a,b的夹角为60°,|a|=2,|b|=1,则|a+2b|=________.
答案 2eq \r(3)
3.已知向量a,b满足3|a|=2|b|=6,且(a-2b)⊥(2a+b),则a,b夹角的余弦值为________.
答案 -eq \f(5,9)
解析 设a,b的夹角为θ,
依题意,(a-2b)·(2a+b)=0,
则2a2-3a·b-2b2=0,
故2×4-3×2×3·cs θ-2×32=0,
则cs θ=-eq \f(5,9).
题型一 平面向量数量积的基本运算
例1 (1)(2021·北京)a=(2,1),b=(2,-1),c=(0,1),则(a+b)·c=_________;a·b=________.
答案 0 3
解析 ∵a=(2,1),b=(2,-1),c=(0,1),
∴a+b=(4,0),
∴(a+b)·c=4×0+0×1=0,
a·b=2×2+1×(-1)=3.
(2)(2022·广州模拟)在平面四边形ABCD中,已知eq \(AB,\s\up6(→))=eq \(DC,\s\up6(→)),P为CD上一点,eq \(CP,\s\up6(→))=3eq \(PD,\s\up6(→)),|eq \(AB,\s\up6(→))|
=4,|eq \(AD,\s\up6(→))|=3,eq \(AB,\s\up6(→))与eq \(AD,\s\up6(→))的夹角为θ,且cs θ=eq \f(2,3),则eq \(AP,\s\up6(→))·eq \(PB,\s\up6(→))=________.
答案 -2
解析 如图所示,
∵eq \(AB,\s\up6(→))=eq \(DC,\s\up6(→)),
∴四边形ABCD为平行四边形,
∵eq \(CP,\s\up6(→))=3eq \(PD,\s\up6(→)),
∴eq \(AP,\s\up6(→))=eq \(AD,\s\up6(→))+eq \(DP,\s\up6(→))=eq \f(1,4)eq \(AB,\s\up6(→))+eq \(AD,\s\up6(→)),
eq \(PB,\s\up6(→))=eq \(AB,\s\up6(→))-eq \(AP,\s\up6(→))=eq \f(3,4)eq \(AB,\s\up6(→))-eq \(AD,\s\up6(→)),
又∵|eq \(AB,\s\up6(→))|=4,|eq \(AD,\s\up6(→))|=3,
cs θ=eq \f(2,3),
则eq \(AB,\s\up6(→))·eq \(AD,\s\up6(→))=4×3×eq \f(2,3)=8,
∴eq \(AP,\s\up6(→))·eq \(PB,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(\(AD,\s\up6(→))+\f(1,4)\(AB,\s\up6(→))))·eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,4)\(AB,\s\up6(→))-\(AD,\s\up6(→))))
=eq \f(1,2)eq \(AB,\s\up6(→))·eq \(AD,\s\up6(→))-eq \(AD,\s\up6(→))2+eq \f(3,16)eq \(AB,\s\up6(→))2
=eq \f(1,2)×8-9+eq \f(3,16)×42=-2.
教师备选
1.(2019·全国Ⅱ)已知eq \(AB,\s\up6(→))=(2,3),eq \(AC,\s\up6(→))=(3,t),|eq \(BC,\s\up6(→))|=1,则eq \(AB,\s\up6(→))·eq \(BC,\s\up6(→))等于( )
A.-3 B.-2 C.2 D.3
答案 C
解析 因为eq \(BC,\s\up6(→))=eq \(AC,\s\up6(→))-eq \(AB,\s\up6(→))=(1,t-3),
所以|eq \(BC,\s\up6(→))|=eq \r(12+t-32)=1,
解得t=3,
所以eq \(BC,\s\up6(→))=(1,0),
所以eq \(AB,\s\up6(→))·eq \(BC,\s\up6(→))=2×1+3×0=2.
2.在边长为2的正三角形ABC中,M是BC的中点,D是线段AM的中点.①若eq \(BD,\s\up6(→))=xeq \(BA,\s\up6(→))+yeq \(BC,\s\up6(→)),则x+y=________;②eq \(BD,\s\up6(→))·eq \(BM,\s\up6(→))=________.
答案 eq \f(3,4) 1
解析 ①∵M是BC的中点,
∴eq \(BM,\s\up6(→))=eq \f(1,2)eq \(BC,\s\up6(→)),
∵D是AM的中点,
∴eq \(BD,\s\up6(→))=eq \f(1,2)eq \(BA,\s\up6(→))+eq \f(1,2)eq \(BM,\s\up6(→))=eq \f(1,2)eq \(BA,\s\up6(→))+eq \f(1,4)eq \(BC,\s\up6(→)),
∴x=eq \f(1,2),y=eq \f(1,4),∴x+y=eq \f(3,4).
②∵△ABC是边长为2的正三角形,M是BC的中点,
∴AM⊥BC,且BM=1,
∴eq \(BD,\s\up6(→))·eq \(BM,\s\up6(→))=|eq \(BD,\s\up6(→))||eq \(BM,\s\up6(→))|cs∠DBM=|eq \(BM,\s\up6(→))|2=1.
思维升华 计算平面向量数量积的主要方法
(1)利用定义:a·b=|a||b|cs〈a,b〉.
(2)利用坐标运算,若a=(x1,y1),b=(x2,y2),则a·b=x1x2+y1y2.
(3)灵活运用平面向量数量积的几何意义.
跟踪训练1 (1)(2021·新高考全国Ⅱ)已知向量a+b+c=0,|a|=1,|b|=|c|=2,a·b+b·c+c·a=________.
答案 -eq \f(9,2)
解析 由已知可得(a+b+c)2
=a2+b2+c2+2(a·b+b·c+c·a)
=9+2(a·b+b·c+c·a)=0,
因此a·b+b·c+c·a=-eq \f(9,2).
(2)(2020·北京)已知正方形ABCD的边长为2,点P满足eq \(AP,\s\up6(→))=eq \f(1,2)(eq \(AB,\s\up6(→))+eq \(AC,\s\up6(→))),则|eq \(PD,\s\up6(→))|=________;eq \(PB,\s\up6(→))·eq \(PD,\s\up6(→))=________.
答案 eq \r(5) -1
解析 建立如图所示的平面直角坐标系,
∵eq \(AP,\s\up6(→))=eq \f(1,2)(eq \(AB,\s\up6(→))+eq \(AC,\s\up6(→))),
∴P为BC的中点.
∴点P的坐标为(2,1),点D的坐标为(0,2),点B的坐标为(2,0),
∴|eq \(PD,\s\up6(→))|=eq \r(5),eq \(PB,\s\up6(→))=(0,-1),eq \(PD,\s\up6(→))=(-2,1),
∴eq \(PB,\s\up6(→))·eq \(PD,\s\up6(→))=-1.
题型二 平面向量数量积的应用
命题点1 向量的模
例2 已知向量a,b满足|a|=6,|b|=4,且a与b的夹角为60°,则|a+b|=____________,|a-3b|=________.
答案 2eq \r(19) 6eq \r(3)
解析 因为|a|=6,|b|=4,a与b的夹角为60°,
所以a·b=|a||b|cs〈a,b〉=6×4×eq \f(1,2)=12,
(a+b)2=a2+2a·b+b2=36+24+16=76,
(a-3b)2=a2-6a·b+9b2=36-72+144
=108,
所以|a+b|=2eq \r(19),|a-3b|=6eq \r(3).
命题点2 向量的夹角
例3 (2020·全国Ⅲ)已知向量a,b满足|a|=5,|b|=6,a·b=-6,则cs〈a,a+b〉等于( )
A.-eq \f(31,35) B.-eq \f(19,35) C.eq \f(17,35) D.eq \f(19,35)
答案 D
解析 ∵|a+b|2=(a+b)2=a2+2a·b+b2
=25-12+36=49,
∴|a+b|=7,
∴cs〈a,a+b〉=eq \f(a·a+b,|a||a+b|)=eq \f(a2+a·b,|a||a+b|)
=eq \f(25-6,5×7)=eq \f(19,35).
命题点3 向量的垂直
例4 (2021·全国乙卷)已知向量a=(1,3),b=(3,4),若(a-λb)⊥b,则λ=________.
答案 eq \f(3,5)
解析 方法一 a-λb=(1-3λ,3-4λ),
∵(a-λb)⊥b,∴(a-λb)·b=0,
即(1-3λ,3-4λ)·(3,4)=0,
∴3-9λ+12-16λ=0,解得λ=eq \f(3,5).
方法二 由(a-λb)⊥b可知,(a-λb)·b=0,即a·b-λb2=0,
从而λ=eq \f(a·b,b2)=eq \f(1,3·3,4,32+42)=eq \f(15,25)=eq \f(3,5).
教师备选
1.已知非零向量a,b满足|a|=2|b|,且(a-b)⊥b,则a与b的夹角为( )
A.eq \f(π,6) B.eq \f(π,3) C.eq \f(2π,3) D.eq \f(5π,6)
答案 B
解析 设a与b的夹角为α,
∵(a-b)⊥b,
∴(a-b)·b=0,
∴a·b=b2,
∴|a|·|b|cs α=|b|2,又|a|=2|b|,
∴cs α=eq \f(1,2),∵α∈[0,π],
∴α=eq \f(π,3).
2.已知e1,e2是两个单位向量,且|e1+e2|=eq \r(3),则|e1-e2|=________.
答案 1
解析 由|e1+e2|=eq \r(3),两边平方,
得eeq \\al(2,1)+2e1·e2+eeq \\al(2,2)=3.又e1,e2是单位向量,
所以2e1·e2=1,
所以|e1-e2|2=eeq \\al(2,1)-2e1·e2+eeq \\al(2,2)=1,
所以|e1-e2|=1.
思维升华 (1)求平面向量的模的方法
①公式法:利用|a|=eq \r(a·a)及(a±b)2=|a|2±2a·b+|b|2,把向量的模的运算转化为数量积运算;
②几何法:利用向量的几何意义,即利用向量线性运算的平行四边形法则或三角形法则作出所求向量,再利用余弦定理等方法求解.
(2)求平面向量的夹角的方法
①定义法:cs θ=eq \f(a·b,|a||b|),求解时应求出a·b,|a|,|b|的值或找出这三个量之间的关系;
②坐标法.
(3)两个向量垂直的充要条件
a⊥b⇔a·b=0⇔|a-b|=|a+b|(其中a≠0,b≠0).
跟踪训练2 (1)已知单位向量a,b满足a·b=0,若向量c=eq \r(7)a+eq \r(2)b,则sin〈a,c〉等于( )
A.eq \f(\r(7),3) B.eq \f(\r(2),3) C.eq \f(\r(7),9) D.eq \f(\r(2),9)
答案 B
解析 方法一 设a=(1,0),b=(0,1),
则c=(eq \r(7),eq \r(2)),
∴cs〈a,c〉=eq \f(a·c,|a||c|)=eq \f(\r(7),3),
∴sin〈a,c〉=eq \f(\r(2),3).
方法二 a·c=a·(eq \r(7)a+eq \r(2)b)
=eq \r(7)a2+eq \r(2)a·b=eq \r(7),
|c|=eq \r(\r(7)a+\r(2)b2)=eq \r(7a2+2b2+2\r(14)a·b)=eq \r(7+2)=3,
∴cs〈a,c〉=eq \f(a·c,|a||c|)=eq \f(\r(7),1×3)=eq \f(\r(7),3),
∴sin〈a,c〉=eq \f(\r(2),3).
(2)(多选)(2021·新高考全国Ⅰ)已知O为坐标原点,点P1(cs α,sin α),P2(cs β,-sin β),P3(cs(α+β),sin(α+β)),A(1,0),则( )
A.|eq \(OP1,\s\up6(—→))|=|eq \(OP2,\s\up6(—→))|
B.|eq \(AP1,\s\up6(—→))|=|eq \(AP2,\s\up6(—→))|
C.eq \(OA,\s\up6(→))·eq \(OP3,\s\up6(—→))=eq \(OP1,\s\up6(—→))·eq \(OP2,\s\up6(—→))
D.eq \(OA,\s\up6(→))·eq \(OP1,\s\up6(—→))=eq \(OP2,\s\up6(—→))·eq \(OP3,\s\up6(—→))
答案 AC
解析 由题意可知,
|eq \(OP1,\s\up6(—→))|=eq \r(cs2α+sin2α)=1,
|eq \(OP2,\s\up6(—→))|=eq \r(cs2β+-sin β2)=1,
所以|eq \(OP1,\s\up6(—→))|=|eq \(OP2,\s\up6(—→))|,故A正确;
取α=eq \f(π,4),则P1eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2),\f(\r(2),2))),
取β=eq \f(5π,4),
则P2eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(\r(2),2),\f(\r(2),2))),
则|eq \(AP1,\s\up6(—→))|≠|eq \(AP2,\s\up6(—→))|,故B错误;
因为eq \(OA,\s\up6(→))·eq \(OP3,\s\up6(—→))=cs(α+β),
eq \(OP1,\s\up6(—→))·eq \(OP2,\s\up6(—→))=cs αcs β-sin αsin β=cs(α+β),
所以eq \(OA,\s\up6(→))·eq \(OP3,\s\up6(—→))=eq \(OP1,\s\up6(—→))·eq \(OP2,\s\up6(—→)),故C正确;
因为eq \(OA,\s\up6(→))·eq \(OP1,\s\up6(—→))=cs α,
eq \(OP2,\s\up6(—→))·eq \(OP3,\s\up6(—→))=cs βcs(α+β)-sin βsin(α+β)
=cs(α+2β),
取α=eq \f(π,4),β=eq \f(π,4),
则eq \(OA,\s\up6(—→))·eq \(OP1,\s\up6(—→))=eq \f(\r(2),2),eq \(OP2,\s\up6(—→))·eq \(OP3,\s\up6(—→))=cs eq \f(3π,4)=-eq \f(\r(2),2),
所以eq \(OA,\s\up6(→))·eq \(OP1,\s\up6(—→))≠eq \(OP2,\s\up6(—→))·eq \(OP3,\s\up6(—→)),故D错误.
题型三 平面向量的实际应用
例5 (多选)(2022·东莞模拟)在日常生活中,我们会看到两个人共提一个行李包的情况(如图所示).假设行李包所受的重力为G,所受的两个拉力分别为F1,F2,若|F1|=|F2|,且F1与F2的夹角为θ,则以下结论正确的是( )
A.|F1|的最小值为eq \f(1,2)|G|
B.θ的范围为[0,π]
C.当θ=eq \f(π,2)时,|F1|=eq \f(\r(2),2)|G|
D.当θ=eq \f(2π,3)时,|F1|=|G|
答案 ACD
解析 由题意知,F1+F2+G=0,
可得F1+F2=-G,两边同时平方得
|G|2=|F1|2+|F2|2+2|F1||F2|cs θ
=2|F1|2+2|F1|2cs θ,
所以|F1|2=eq \f(|G|2,21+cs θ).
当θ=0时,|F1|min=eq \f(1,2)|G|;
当θ=eq \f(π,2)时,|F1|=eq \f(\r(2),2)|G|;
当θ=eq \f(2π,3)时,|F1|=|G|,故A,C,D正确;
当θ=π时,竖直方向上没有分力与重力平衡,不成立,所以θ∈[0,π),故B错误.
教师备选
若平面上的三个力F1,F2,F3作用于一点,且处于平衡状态,已知|F1|=1 N,|F2|=eq \f(\r(6)+\r(2),2) N,F1与F2的夹角为45°,求:
(1)F3的大小;
(2)F3与F1夹角的大小.
解 (1)∵三个力平衡,
∴F1+F2+F3=0,
∴|F3|=|F1+F2|=eq \r(|F1|2+2F1·F2+|F2|2)
=eq \r(12+2×1×\f(\r(6)+\r(2),2)cs 45°+\b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(6)+\r(2),2)))2)
=eq \r(4+2\r(3))=1+eq \r(3).
(2)方法一 设F3与F1的夹角为θ,
则|F2|=eq \r(|F1|2+|F3|2+2|F1||F3|cs θ),
即eq \f(\r(6)+\r(2),2)=eq \r(12+1+\r(3)2+2×1×1+\r(3)cs θ),
解得cs θ=-eq \f(\r(3),2),
∵θ∈[0,π],
∴θ=eq \f(5π,6).
方法二 设F3与F1的夹角为θ,
由余弦定理得
cs(π-θ)=eq \f(12+1+\r(3)2-\b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(6)+\r(2),2)))2,2×1×1+\r(3))=eq \f(\r(3),2),
∵θ∈[0,π],∴θ=eq \f(5π,6).
思维升华 用向量方法解决实际问题的步骤
跟踪训练3 (2022·沈阳二中模拟)渭河某处南北两岸平行,如图所示,某艘游船从南岸码头A出发航行到北岸,假设游船在静水中航行速度的大小为|ν1|=10 km/h,水流速度的大小为|ν2|=6 km/h.设ν1与ν2的夹角为120°,北岸的点A′在码头A的正北方向,那么该游船航行到北岸的位置应( )
A.在A′东侧 B.在A′西侧
C.恰好与A′重合 D.无法确定
答案 A
解析 建立如图所示的平面直角坐标系,
由题意可得ν1=(-5,5eq \r(3)),ν2=(6,0),
所以ν1+ν2=(1,5eq \r(3)),
说明游船有x轴正方向的速度,即向东的速度,所以该游船航行到北岸的位置应在A′东侧.
极化恒等式:设a,b为两个平面向量,则有恒等式a·b=eq \f(1,4)eq \b\lc\[\rc\](\a\vs4\al\c1(a+b2-a-b2)).
如图所示.
(1)在平行四边形ABDC中,eq \(AB,\s\up6(→))=a,eq \(AC,\s\up6(→))=b,则a·b=eq \f(1,4)(|eq \(AD,\s\up6(→))|2-|eq \(BC,\s\up6(→))|2).
(2)在△ABC中,eq \(AB,\s\up6(→))=a,eq \(AC,\s\up6(→))=b,AM为中线,则a·b=|eq \(AM,\s\up6(→))|2-eq \f(1,4)|eq \(BC,\s\up6(→))|2.
例1 在△ABC中,M是BC的中点,AM=3,BC=10,则eq \(AB,\s\up6(→))·eq \(AC,\s\up6(→))=________.
答案 -16
解析 如图所示,由极化恒等式,易得eq \(AB,\s\up6(→))·eq \(AC,\s\up6(→))=eq \(AM,\s\up6(→))2-eq \(MB,\s\up6(→))2=32-52=-16.
例2 已知AB为圆x2+y2=1的一条直径,点P为直线x-y+2=0上任意一点,则eq \(PA,\s\up6(→))·eq \(PB,\s\up6(→))的最小值是________.
答案 1
解析 如图所示,由极化恒等式易知,当OP垂直于直线x-y+2=0时,eq \(PA,\s\up6(→))·eq \(PB,\s\up6(→))有最小值,即
eq \(PA,\s\up6(→))·eq \(PB,\s\up6(→))=eq \(PO,\s\up6(→))2-eq \(OB,\s\up6(→))2=(eq \r(2))2-12=1.
例3 已知a,b是平面内两个互相垂直的单位向量,若向量c满足(a-c)·(b-c)=0,则|c|的最大值是( )
A.1 B.2 C.eq \r(2) D.eq \f(\r(2),2)
答案 C
解析 如图所示,
设eq \(OA,\s\up6(→))⊥eq \(OB,\s\up6(→)),
记eq \(OA,\s\up6(→))=a,eq \(OB,\s\up6(→))=b,eq \(OC,\s\up6(→))=c,
M为AB的中点,
由极化恒等式有
(a-c)·(b-c)=eq \(CA,\s\up6(→))·eq \(CB,\s\up6(→))
=|eq \(CM,\s\up6(→))|2-eq \f(|\(AB,\s\up6(→))|2,4)=0,
∴|eq \(CM,\s\up6(→))|2=eq \f(|\(AB,\s\up6(→))|2,4)=eq \f(1,2),
可知eq \(MC,\s\up6(→))是有固定起点,固定模长的动向量.
点C的轨迹是以AB为直径的圆,且点O也在此圆上,
所以|c|的最大值为圆的直径长,即为eq \r(2).
课时精练
1.(2020·全国Ⅱ)已知单位向量a,b的夹角为60°,则在下列向量中,与b垂直的是( )
A.a+2b B.2a+b C.a-2b D.2a-b
答案 D
解析 由题意得|a|=|b|=1,
设a,b的夹角为θ=60°,
故a·b=|a||b|cs θ=eq \f(1,2).
对A项,(a+2b)·b=a·b+2b2
=eq \f(1,2)+2=eq \f(5,2)≠0;
对B项,(2a+b)·b=2a·b+b2
=2×eq \f(1,2)+1=2≠0;
对C项,(a-2b)·b=a·b-2b2
=eq \f(1,2)-2=-eq \f(3,2)≠0;
对D项,(2a-b)·b=2a·b-b2=2×eq \f(1,2)-1=0.
2.(2022·石家庄模拟)已知向量a=(2,-2),b=(2,1),b∥c,a·c=4,则|c|等于( )
A.2eq \r(5) B.4
C.5eq \r(2) D.4eq \r(2)
答案 A
解析 因为b∥c,
所以c=λb=(2λ,λ)(λ∈R),
又a·c=4λ-2λ=2λ=4,
所以λ=2,c=(4,2),|c|=eq \r(42+22)=2eq \r(5).
3.(2022·沈阳模拟)若两个非零向量a,b满足|a+b|=|a-b|=2|a|,则a-b与b的夹角为( )
A.eq \f(π,6) B.eq \f(π,3) C.eq \f(2π,3) D.eq \f(5π,6)
答案 D
解析 |a+b|=|a-b|=2|a|,等号左右同时平方,
得|a+b|2=|a-b|2=4|a|2,即|a|2+|b|2+2a·b=|a|2+|b|2-2a·b=4|a|2,
所以a·b=0且|b|2=3|a|2,
所以|a-b|=eq \r(|a-b|2)
=eq \r(|a|2+|b|2-2a·b)=eq \f(2\r(3),3)|b|,
所以cs〈a-b,b〉=eq \f(a-b·b,|a-b||b|)
=eq \f(-|b|2,\f(2\r(3),3)|b|·|b|)=-eq \f(\r(3),2),
因为〈a-b,b〉∈[0,π],所以〈a-b,b〉=eq \f(5π,6).
4.已知a=(-2,1),b=(k,-3),c=(1,2),若(a-2b)⊥c,则与b共线的单位向量为( )
A.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2\r(5),5),-\f(\r(5),5)))或eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(2\r(5),5),\f(\r(5),5)))
B.eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(2\r(5),5),-\f(\r(5),5)))或eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2\r(5),5),\f(\r(5),5)))
C.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2\r(5),5),\f(\r(5),5)))
D.eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(2\r(5),5),\f(\r(5),5)))
答案 A
解析 由题意得a-2b=(-2-2k,7),
∵(a-2b)⊥c,
∴(a-2b)·c=0,
即(-2-2k,7)·(1,2)=0,-2-2k+14=0,
解得k=6,
∴b=(6,-3),
∴e=±eq \f(b,\r(62+-32))=±eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2\r(5),5),-\f(\r(5),5))).
5.(多选)(2022·盐城模拟)下列关于向量a,b,c的运算,一定成立的有( )
A.(a+b)·c=a·c+b·c
B.(a·b)·c=a·(b·c)
C.a·b≤|a|·|b|
D.|a-b|≤|a|+|b|
答案 ACD
解析 根据数量积的分配律可知A正确;
选项B中,左边为c的共线向量,右边为a的共线向量,故B不正确;
根据数量积的定义,可知a·b=|a||b|cs〈a,b〉≤|a|·|b|,故C正确;
|a-b|2=|a|2+|b|2-2a·b=|a|2+|b|2-2|a||b|·cs〈a,b〉≤|a|2+|b|2+2|a||b|=(|a|+|b|)2,
故|a-b|≤|a|+|b|,故D正确.
6.(多选)已知向量a=(2,1),b=(1,-1),c=(m-2,-n),其中m,n均为正数,且(a-b)∥c,则下列说法正确的是( )
A.a与b的夹角为钝角
B.向量a在b上的投影向量为eq \f(\r(2),2)b
C.2m+n=4
D.mn的最大值为2
答案 CD
解析 对于A,向量a=(2,1),b=(1,-1),
则a·b=2-1=1>0,
又a,b不共线,
所以a,b的夹角为锐角,故A错误;
对于B,向量a在b上的投影向量为
eq \f(a·b,|b|)·eq \f(b,|b|)=eq \f(1,2)b,B错误;
对于C,a-b=(1,2),若(a-b)∥c,
则-n=2(m-2),变形可得2m+n=4,C正确;
对于D,由2m+n=4,且m,n均为正数,
得mn=eq \f(1,2)(2m·n)≤eq \f(1,2)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2m+n,2)))2=2,当且仅当m=1,n=2时,等号成立,即mn的最大值为2,D正确.
7.(2021·全国甲卷)已知向量a=(3,1),b=(1,0),c=a+kb.若a⊥c,则k=________.
答案 -eq \f(10,3)
解析 c=(3,1)+(k,0)=(3+k,1),a·c=3(3+k)+1×1=10+3k=0,得k=-eq \f(10,3).
8.(2020·全国Ⅰ)设a,b为单位向量,且|a+b|=1,则|a-b|=________.
答案 eq \r(3)
解析 将|a+b|=1两边平方,得a2+2a·b+b2=1.
∵a2=b2=1,
∴1+2a·b+1=1,即2a·b=-1.
∴|a-b|=eq \r(a-b2)=eq \r(a2-2a·b+b2)
=eq \r(1--1+1)=eq \r(3).
9.(2022·长沙模拟)在△ABC中,BC的中点为D,设向量eq \(AB,\s\up6(→))=a,eq \(AC,\s\up6(→))=b.
(1)用a,b表示向量eq \(AD,\s\up6(→));
(2)若向量a,b满足|a|=3,|b|=2,〈a,b〉=60°,求eq \(AB,\s\up6(→))·eq \(AD,\s\up6(→))的值.
解 (1)eq \(AD,\s\up6(→))=eq \f(1,2)(eq \(AB,\s\up6(→))+eq \(AC,\s\up6(→)))
=eq \f(1,2)a+eq \f(1,2)b,
所以eq \(AD,\s\up6(→))=eq \f(1,2)a+eq \f(1,2)b.
(2)eq \(AB,\s\up6(→))·eq \(AD,\s\up6(→))=a·eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)a+\f(1,2)b))
=eq \f(1,2)a2+eq \f(1,2)a·b
=eq \f(1,2)×32+eq \f(1,2)×3×2×cs 60°=6,
所以eq \(AB,\s\up6(→))·eq \(AD,\s\up6(→))=6.
10.(2022·湛江模拟)已知向量m=(eq \r(3)sin x,cs x-1),n=(cs x,cs x+1),若f(x)=m·n.
(1)求函数f(x)的单调递增区间;
(2)在Rt△ABC中,角A,B,C的对边分别为a,b,c,若∠A=90°,f(C)=0,c=eq \r(3),CD为∠BCA的角平分线,E为CD的中点,求BE的长.
解 (1)f(x)=m·n
=eq \r(3)sin x·cs x+cs2x-1
=eq \f(\r(3),2)sin 2x+eq \f(1,2)cs 2x-eq \f(1,2)
=sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x+\f(π,6)))-eq \f(1,2).
令2x+eq \f(π,6)∈eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ-\f(π,2),2kπ+\f(π,2)))(k∈Z),
则x∈eq \b\lc\[\rc\](\a\vs4\al\c1(kπ-\f(π,3),kπ+\f(π,6)))(k∈Z).
所以函数f(x)的单调递增区间为
eq \b\lc\[\rc\](\a\vs4\al\c1(kπ-\f(π,3),kπ+\f(π,6)))(k∈Z).
(2)f(C)=sineq \b\lc\(\rc\)(\a\vs4\al\c1(2C+\f(π,6)))-eq \f(1,2)=0,
sineq \b\lc\(\rc\)(\a\vs4\al\c1(2C+\f(π,6)))=eq \f(1,2),又C∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0,\f(π,2))),
所以C=eq \f(π,3).
在△ACD中,CD=eq \f(2\r(3),3),
在△BCE中,
BE=eq \r(22+\b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),3)))2-2×2×\f(\r(3),3)×\f(\r(3),2))=eq \f(\r(21),3).
11.(2022·黄冈质检)圆内接四边形ABCD中,AD=2,CD=4,BD是圆的直径,则eq \(AC,\s\up6(→))·eq \(BD,\s\up6(→))等于( )
A.12 B.-12
C.20 D.-20
答案 B
解析 如图所示,由题知∠BAD=∠BCD=90°,AD=2,CD=4,
∴eq \(AC,\s\up6(→))·eq \(BD,\s\up6(→))=(eq \(AD,\s\up6(→))+eq \(DC,\s\up6(→)))·eq \(BD,\s\up6(→))
=eq \(AD,\s\up6(→))·eq \(BD,\s\up6(→))+eq \(DC,\s\up6(→))·eq \(BD,\s\up6(→))
=|eq \(AD,\s\up6(→))||eq \(BD,\s\up6(→))|cs∠BDA-|eq \(DC,\s\up6(→))||eq \(BD,\s\up6(→))|cs∠BDC
=|eq \(AD,\s\up6(→))|2-|eq \(DC,\s\up6(→))|2=4-16=-12.
12.在△ABC中,已知eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\(AB,\s\up6(→)),|\(AB,\s\up6(→))|)+\f(\(AC,\s\up6(→)),|\(AC,\s\up6(→))|)))·eq \(BC,\s\up6(→))=0,且eq \f(\(AB,\s\up6(→)),|\(AB,\s\up6(→))|)·eq \f(\(AC,\s\up6(→)),|\(AC,\s\up6(→))|)=eq \f(1,2),则△ABC为( )
A.等边三角形
B.直角三角形
C.等腰三角形
D.三边均不相等的三角形
答案 A
解析 eq \f(\(AB,\s\up6(→)),|\(AB,\s\up6(→))|),eq \f(\(AC,\s\up6(→)),|\(AC,\s\up6(→))|)分别为与eq \(AB,\s\up6(→)),eq \(AC,\s\up6(→))方向相同的单位向量,由平行四边形法则可知向量eq \f(\(AB,\s\up6(→)),|\(AB,\s\up6(→))|)+eq \f(\(AC,\s\up6(→)),|\(AC,\s\up6(→))|)所在的直线为∠BAC的平分线.
因为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\(AB,\s\up6(→)),|\(AB,\s\up6(→))|)+\f(\(AC,\s\up6(→)),|\(AC,\s\up6(→))|)))·eq \(BC,\s\up6(→))=0,
所以∠BAC的平分线垂直于BC,
所以AB=AC.
又eq \f(\(AB,\s\up6(→)),|\(AB,\s\up6(→))|)·eq \f(\(AC,\s\up6(→)),|\(AC,\s\up6(→))|)=eq \b\lc\|\rc\|(\a\vs4\al\c1(\f(\(AB,\s\up6(→)),|\(AB,\s\up6(→))|)))eq \b\lc\|\rc\|(\a\vs4\al\c1(\f(\(AC,\s\up6(→)),|\(AC,\s\up6(→))|)))·cs∠BAC
=eq \f(1,2),
所以cs∠BAC=eq \f(1,2),∠BAC=60°.
所以△ABC为等边三角形.
13.(2022·潍坊模拟)如图所示,一个物体被两根轻质细绳拉住,且处于平衡状态,已知两条绳上的拉力分别是F1,F2,且F1,F2与水平夹角均为45°,|F1|=|F2|=10eq \r(2) N,则物体的重力大小为________ N.
答案 20
解析 如图所示,∵|F1|=|F2|=10eq \r(2) N,
∴|F1+F2|=10eq \r(2)×eq \r(2)=20 N,
∴物体的重力大小为20 N.
14.(2021·天津)在边长为1的等边三角形ABC中,D为线段BC上的动点,DE⊥AB且交AB于点E,DF∥AB且交AC于点F,则|2eq \(BE,\s\up6(→))+eq \(DF,\s\up6(→))|的值为________;(eq \(DE,\s\up6(→))+eq \(DF,\s\up6(→)))·eq \(DA,\s\up6(→))的最小值为________.
答案 1 eq \f(11,20)
解析 设BE=x,x∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0,\f(1,2))),
∵△ABC为边长为1的等边三角形,DE⊥AB,
∴∠BDE=30°,BD=2x,DE=eq \r(3)x,
DC=1-2x,
∵DF∥AB,∴△DFC为边长为1-2x的等边三角形,DE⊥DF,
∴(2eq \(BE,\s\up6(→))+eq \(DF,\s\up6(→)))2=4eq \(BE,\s\up6(→))2+4eq \(BE,\s\up6(→))·eq \(DF,\s\up6(→))+eq \(DF,\s\up6(→))2=4x2+4x(1-2x)×cs 0°+(1-2x)2=1,
∴|2eq \(BE,\s\up6(→))+eq \(DF,\s\up6(→))|=1,
∵(eq \(DE,\s\up6(→))+eq \(DF,\s\up6(→)))·eq \(DA,\s\up6(→))=(eq \(DE,\s\up6(→))+eq \(DF,\s\up6(→)))·(eq \(DE,\s\up6(→))+eq \(EA,\s\up6(→)))=eq \(DE,\s\up6(→))2+eq \(DF,\s\up6(→))·eq \(EA,\s\up6(→))=(eq \r(3)x)2+(1-2x)×(1-x)=5x2-3x+1=5eq \b\lc\(\rc\)(\a\vs4\al\c1(x-\f(3,10)))2+eq \f(11,20),
∴当x=eq \f(3,10)时,(eq \(DE,\s\up6(→))+eq \(DF,\s\up6(→)))·eq \(DA,\s\up6(→))的最小值为eq \f(11,20).
15.(多选)定义一种向量运算“⊗”:a⊗b=eq \b\lc\{\rc\ (\a\vs4\al\c1(a·b,当a,b不共线时,,|a-b|,当a,b共线时))(a,b是任意的两个向量).对于同一平面内的向量a,b,c,e,给出下列结论,正确的是( )
A.a⊗b=b⊗a
B.λ(a⊗b)=(λa)⊗b(λ∈R)
C.(a+b)⊗c=a⊗c+b⊗c
D.若e是单位向量,则|a⊗e|≤|a|+1
答案 AD
解析 当a,b共线时,a⊗b=|a-b|=|b-a|=b⊗a,当a,b不共线时,a⊗b=a·b=b·a=b⊗a,故A正确;
当λ=0,b≠0时,λ(a⊗b)=0,(λa)⊗b=|0-b|≠0,故B错误;
当a+b与c共线时,则存在a,b与c不共线,(a+b)⊗c=|a+b-c|,a⊗c+b⊗c=a·c+b·c,显然|a+b-c|≠a·c+b·c,故C错误;
当e与a不共线时,|a⊗e|=|a·e|<|a|·|e|<|a|+1,当e与a共线时,设a=ue,u∈R,|a⊗e|=|a-e|=|ue-e|=|u-1|≤|u|+1,故D正确.
16.已知在△ABC中,角A,B,C的对边分别为a,b,c,向量m=(sin A,sin B),n=
(cs B,cs A),m·n=sin 2C.
(1)求角C的大小;
(2)若sin A,sin C,sin B成等差数列,且eq \(CA,\s\up6(→))·(eq \(AB,\s\up6(→))-eq \(AC,\s\up6(→)))=18,求c.
解 (1)m·n=sin Acs B+sin Bcs A
=sin(A+B),
在△ABC中,A+B=π-C,0
所以m·n=sin C,
又m·n=sin 2C,
所以sin 2C=sin C,cs C=eq \f(1,2),
又因为C∈(0,π),故C=eq \f(π,3).
(2)由sin A,sin C,sin B成等差数列,
可得2sin C=sin A+sin B,
由正弦定理得2c=a+b.
因为eq \(CA,\s\up6(→))·(eq \(AB,\s\up6(→))-eq \(AC,\s\up6(→)))=18,
所以eq \(CA,\s\up6(→))·eq \(CB,\s\up6(→))=18,
即abcs C=18,ab=36.
由余弦定理得
c2=a2+b2-2abcs C=(a+b)2-3ab,
所以c2=4c2-3×36,c2=36,
所以c=6.几何表示
坐标表示
数量积
a·b=|a||b|cs θ
a·b=x1x2+y1y2
模
|a|=eq \r(a·a)
|a|=eq \r(x\\al(2,1)+y\\al(2,1))
夹角
cs θ=eq \f(a·b,|a||b|)
cs θ=eq \f(x1x2+y1y2,\r(x\\al(2,1)+y\\al(2,1)) \r(x\\al(2,2)+y\\al(2,2)))
a⊥b的充要条件
a·b=0
x1x2+y1y2=0
a∥b的充要条件
a=λb(λ∈R)
x1y2-x2y1=0
|a·b|与|a||b|的关系
|a·b|≤|a||b|
(当且仅当a∥b时等号成立)
|x1x2+y1y2|≤eq \r(x\\al(2,1)+y\\al(2,1)x\\al(2,2)+y\\al(2,2))
(新高考)高考数学一轮复习讲练测第5章§5.3平面向量的数量积(含解析): 这是一份(新高考)高考数学一轮复习讲练测第5章§5.3平面向量的数量积(含解析),共15页。
2024高考数学一轮复习讲义(步步高版)第五章 §5.3 平面向量的数量积: 这是一份2024高考数学一轮复习讲义(步步高版)第五章 §5.3 平面向量的数量积,共15页。
新高考数学一轮复习讲义5.3《平面向量的数量积》(2份打包,解析版+原卷版): 这是一份新高考数学一轮复习讲义5.3《平面向量的数量积》(2份打包,解析版+原卷版),文件包含新高考数学一轮复习讲义53《平面向量的数量积》含详解doc、新高考数学一轮复习讲义53《平面向量的数量积》原卷版doc等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。












