中考压轴题第2部分 抛物线平行四边形 学案

1．（09•江西）如图，抛物线y=﹣x2+2x+3与x轴相交于A、B两点（点A在点B的左侧），与y轴相交于点C，顶点为D．
（1）直接写出A、B、C三点的坐标和抛物线的对称轴；
（2）连接BC，与抛物线的对称轴交于点E，点P为线段BC上的一个动点，过点P作PF∥DE交抛物线于点F，设点P的横坐标为m；
①用含m的代数式表示线段PF的长，并求出当m为何值时，四边形PEDF为平行四边形？
②设△BCF的面积为S，求S与m的函数关系式．









2．（12•东营）已知抛物线经过A（2，0）．设顶点为点P，与x轴的另一交点为点B．
（1）求b的值，求出点P、点B的坐标；
（2）如图，在直线 y=x上是否存在点D，使四边形OPBD为平行四边形？若存在，求出点D的坐标；若不存在，请说明理由；
（3）在x轴下方的抛物线上是否存在点M，使△AMP≌△AMB？如果存在，试举例验证你的猜想；如果不存在，试说明理由．











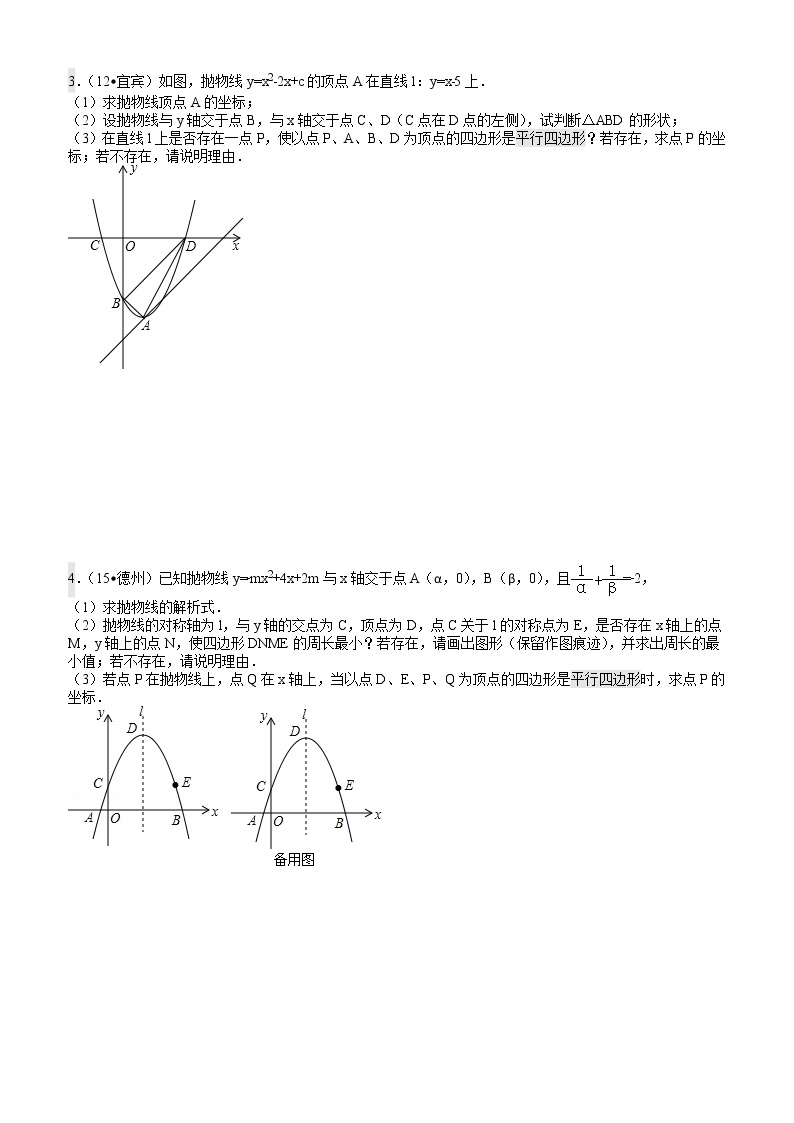
3．（12•宜宾）如图，抛物线y=x2﹣2x+c的顶点A在直线l：y=x﹣5上．
（1）求抛物线顶点A的坐标；
（2）设抛物线与y轴交于点B，与x轴交于点C、D（C点在D点的左侧），试判断△ABD的形状；
（3）在直线l上是否存在一点P，使以点P、A、B、D为顶点的四边形是平行四边形？若存在，求点P的坐标；若不存在，请说明理由．













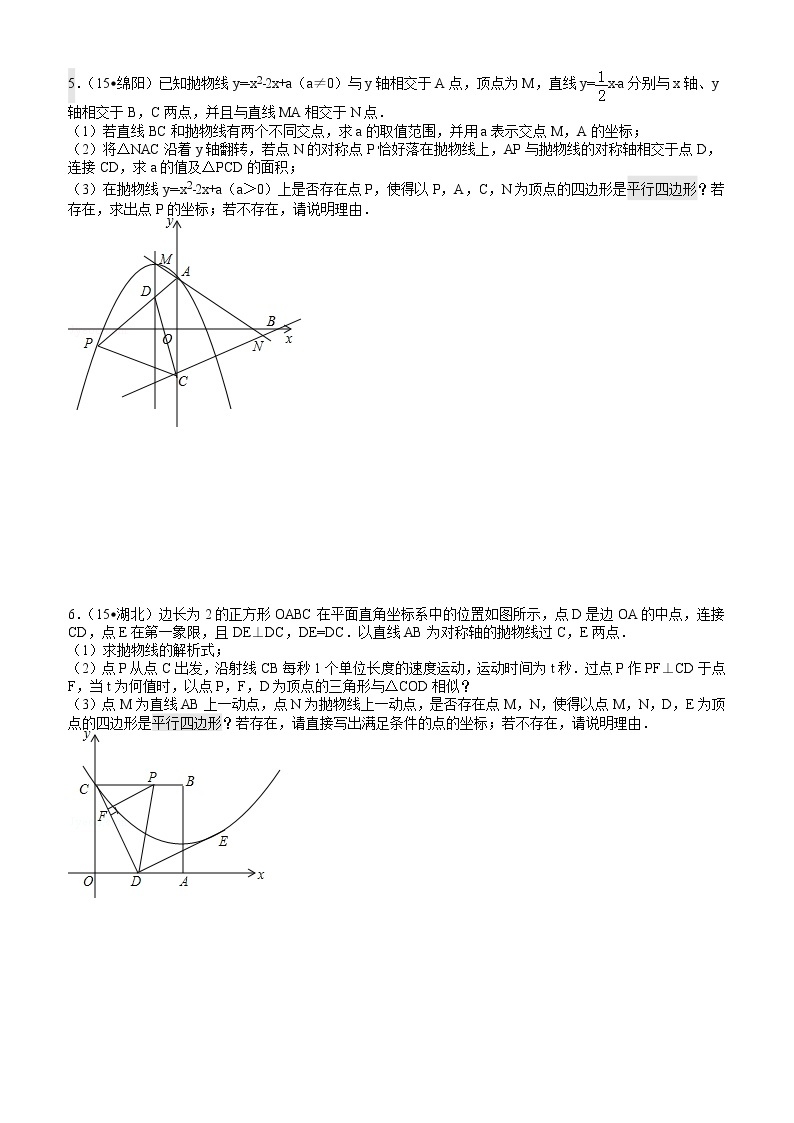
4．（15•德州）已知抛物线y=﹣mx2+4x+2m与x轴交于点A（α，0），B（β，0），且=﹣2，
（1）求抛物线的解析式．
（2）抛物线的对称轴为l，与y轴的交点为C，顶点为D，点C关于l的对称点为E，是否存在x轴上的点M，y轴上的点N，使四边形DNME的周长最小？若存在，请画出图形（保留作图痕迹），并求出周长的最小值；若不存在，请说明理由．
（3）若点P在抛物线上，点Q在x轴上，当以点D、E、P、Q为顶点的四边形是平行四边形时，求点P的坐标．










5．（15•绵阳）已知抛物线y=﹣x2﹣2x+a（a≠0）与y轴相交于A点，顶点为M，直线y=x﹣a分别与x轴、y轴相交于B，C两点，并且与直线MA相交于N点．
（1）若直线BC和抛物线有两个不同交点，求a的取值范围，并用a表示交点M，A的坐标；
（2）将△NAC沿着y轴翻转，若点N的对称点P恰好落在抛物线上，AP与抛物线的对称轴相交于点D，连接CD，求a的值及△PCD的面积；
（3）在抛物线y=﹣x2﹣2x+a（a＞0）上是否存在点P，使得以P，A，C，N为顶点的四边形是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．












6．（15•湖北）边长为2的正方形OABC在平面直角坐标系中的位置如图所示，点D是边OA的中点，连接CD，点E在第一象限，且DE⊥DC，DE=DC．以直线AB为对称轴的抛物线过C，E两点．
（1）求抛物线的解析式；
（2）点P从点C出发，沿射线CB每秒1个单位长度的速度运动，运动时间为t秒．过点P作PF⊥CD于点F，当t为何值时，以点P，F，D为顶点的三角形与△COD相似？
（3）点M为直线AB上一动点，点N为抛物线上一动点，是否存在点M，N，使得以点M，N，D，E为顶点的四边形是平行四边形？若存在，请直接写出满足条件的点的坐标；若不存在，请说明理由．







7．（15•广安）如图，边长为1的正方形ABCD一边AD在x负半轴上，直线l：y=x+2经过点B（x，1）与x轴，y轴分别交于点H，F，抛物线y=﹣x2+bx+c．
（1）求A，D两点的坐标及抛物线经过A，D两点时的解析式；
（2）当抛物线的顶点E（m，n）在直线l上运动时，连接EA，ED，试求△EAD的面积S与m之间的函数解析式，并写出m的取值范围；
（3）设抛物线与y轴交于G点，当顶点E在直线l上运动时，以A，C，E，G为顶点的四边形能否成为平行四边形？若能，求出E点坐标；若不能，请说明理由．











8．（12秋•义乌市校级期中）已知抛物线：
（1）求抛物线y1的顶点坐标．
（2）将抛物线y1向右平移2个单位，再向上平移1个单位，得到抛物线y2，求抛物线y2的解析式．
（3）如图，抛物线y2的顶点为P，x轴上有一动点M，在y1、y2这两条抛物线上是否存在点N，使O（原点）、P、M、N四点构成以OP为一边的平行四边形？若存在，求出N点的坐标；若不存在，请说明理由．










9．（12•襄阳）如图，在矩形OABC中，AO=10，AB=8，沿直线CD折叠矩形OABC的一边BC，使点B落在OA边上的点E处．分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系，抛物线y=ax2+bx+c经过O，D，C三点．
（1）求AD的长及抛物线的解析式；
（2）一动点P从点E出发，沿EC以每秒2个单位长的速度向点C运动，同时动点Q从点C出发，沿CO以每秒1个单位长的速度向点O运动，当点P运动到点C时，两点同时停止运动．设运动时间为t秒，当t为何值时，以P、Q、C为顶点的三角形与△ADE相似？
（3）点N在抛物线对称轴上，点M在抛物线上，是否存在这样的点M与点N，使以M，N，C，E为顶点的四边形是平行四边形？若存在，请直接写出点M与点N的坐标（不写求解过程）；若不存在，请说明理由．










10．（12•恩施州）如图，已知抛物线y=﹣x2+bx+c与一直线相交于A（﹣1，0），C（2，3）两点，与y轴交于点N．其顶点为D．
（1）抛物线及直线AC的函数关系式；
（2）设点M（3，m），求使MN+MD的值最小时m的值；
（3）若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EF∥BD交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由；
（4）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值．








11．（14•赤峰）如图，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣1，0），B（3，0）两点，与y轴交于点C（0，﹣3）．

（1）求该抛物线的解析式及顶点M坐标；
（2）求△BCM面积与△ABC面积的比；
（3）若P是x轴上一个动点，过P作射线PQ∥AC交抛物线于点Q，随着P点的运动，在抛物线上是否存在这样的点Q，使以A，P，Q，C为顶点的四边形为平行四边形？若存在，请求出Q点坐标；若不存在，请说明理由．













12．（14•潍坊）如图，抛物线y=ax2+bx+c（a≠0）与y轴交于点C（0，4），与x轴交于点A和点B，其中点A的坐标为（﹣2，0），抛物线的对称轴x=1与抛物线交于点D，与直线BC交于点E．
（1）求抛物线的解析式；
（2）若点F是直线BC上方的抛物线上的一个动点，是否存在点F使四边形ABFC的面积为17，若存在，求出点F的坐标；若不存在，请说明理由；
（3）平行于DE的一条动直线l与直线BC相交于点P，与抛物线相交于点Q，若以D、E、P、Q为顶点的四边形是平行四边形，求点P的坐标．







13．（14•济宁）如图，抛物线y=x2+bx+c与x轴交于A（5，0）、B（﹣1，0）两点，过点A作直线AC⊥x轴，交直线y=2x于点C；
（1）求该抛物线的解析式；
（2）求点A关于直线y=2x的对称点A′的坐标，判定点A′是否在抛物线上，并说明理由；
（3）点P是抛物线上一动点，过点P作y轴的平行线，交线段CA′于点M，是否存在这样的点P，使四边形PACM是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．













14．（14•东营）如图，直线y=2x+2与x轴交于点A，与y轴交于点B，把△AOB沿y轴翻折，点A落到点C，过点B的抛物线y=﹣x2+bx+c与直线BC交于点D（3，﹣4）．
（1）求直线BD和抛物线的解析式；
（2）在第一象限内的抛物线上，是否存在一点M，作MN垂直于x轴，垂足为点N，使得以M、O、N为顶点的三角形与△BOC相似？若存在，求出点M的坐标；若不存在，请说明理由；
（3）在直线BD上方的抛物线上有一动点P，过点P作PH垂直于x轴，交直线BD于点H，当四边形BOHP是平行四边形时，试求动点P的坐标．







15．（14•山西）综合与探究：如图，在平面直角坐标系xOy中，四边形OABC是平行四边形，A、C两点的坐标分别为（4，0），（﹣2，3），抛物线W经过O、A、C三点，D是抛物线W的顶点．
（1）求抛物线W的解析式及顶点D的坐标；
（2）将抛物线W和▱OABC一起先向右平移4个单位后，再向下平移m（0＜m＜3）个单位，得到抛物线W′和▱O′A′B′C′，在向下平移的过程中，设▱O′A′B′C′与▱OABC的重叠部分的面积为S，试探究：当m为何值时S有最大值，并求出S的最大值；
（3）在（2）的条件下，当S取最大值时，设此时抛物线W′的顶点为F，若点M是x轴上的动点，点N是抛物线W′上的动点，试判断是否存在这样的点M和点N，使得以D、F、M、N为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．











16．（16•南充）如图，抛物线与x轴交于点A（﹣5，0）和点B（3，0）．与y轴交于点C（0，5）．有一宽度为1，长度足够的矩形（阴影部分）沿x轴方向平移，与y轴平行的一组对边交抛物线于点P和Q，交直线AC于点M和N．交x轴于点E和F．
（1）求抛物线的解析式；
（2）当点M和N都在线段AC上时，连接MF，如果sin∠AMF=，求点Q的坐标；
（3）在矩形的平移过程中，当以点P，Q，M，N为顶点的四边形是平行四边形时，求点M的坐标．






17．（16•成都）如图，在平面直角坐标系xOy中，抛物线y=a（x+1）2﹣3与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C（0，﹣），顶点为D，对称轴与x轴交于点H，过点H的直线l交抛物线于P，Q两点，点Q在y轴的右侧．
（1）求a的值及点A，B的坐标；
（2）当直线l将四边形ABCD分为面积比为3：7的两部分时，求直线l的函数表达式；
（3）当点P位于第二象限时，设PQ的中点为M，点N在抛物线上，则以DP为对角线的四边形DMPN能否为菱形？若能，求出点N的坐标；若不能，请说明理由．

　
1.解：（1）A（﹣1，0），B（3，0），C（0，3）．
抛物线的对称轴是：直线x=1．

（2）①设直线BC的函数关系式为：y=kx+b．
把B（3，0），C（0，3）分别代入得：
解得：．
所以直线BC的函数关系式为：y=﹣x+3．
当x=1时，y=﹣1+3=2，
∴E（1，2）．
当x=m时，y=﹣m+3，
∴P（m，﹣m+3）．
在y=﹣x2+2x+3中，当x=1时，y=4．
∴D（1，4）
当x=m时，y=﹣m2+2m+3，
∴F（m，﹣m2+2m+3）
∴线段DE=4﹣2=2，
线段PF=﹣m2+2m+3﹣（﹣m+3）=﹣m2+3m
∵PF∥DE，
∴当PF=ED时，四边形PEDF为平行四边形．
由﹣m2+3m=2，
解得：m1=2，m2=1（不合题意，舍去）．
因此，当m=2时，四边形PEDF为平行四边形．
②设直线PF与x轴交于点M，由B（3，0），O（0，0），
可得：OB=OM+MB=3．
∵S=S△BPF+S△CPF
即S=PF•BM+PF•OM=PF•（BM+OM）=PF•OB．
∴S=×3（﹣m2+3m）=﹣m2+m（0≤m≤3）．

方法二：
（3）∵B（3，0），C（0，3），D（1，4），∴，∴，
∵∠DEC=∠COB=90°，
∴△DEC∽△COB，
∴∠DCE=∠CBO，
∴∠DCE+∠OCB=90°，
∴DC⊥BC，
∴△BCD的外接圆圆心M为BD中点，
∴MX==2，MY==2，
∴△BCD的外接圆圆心M（2，2）．


　
2．（2012•东营）已知抛物线经过A（2，0）．设顶点为点P，与x轴的另一交点为点B．
（1）求b的值，求出点P、点B的坐标；
（2）如图，在直线 y=x上是否存在点D，使四边形OPBD为平行四边形？若存在，求出点D的坐标；若不存在，请说明理由；
（3）在x轴下方的抛物线上是否存在点M，使△AMP≌△AMB？如果存在，试举例验证你的猜想；如果不存在，试说明理由．

【解答】解：（1）由于抛物线经过A（2，0），
所以，
解得．
所以抛物线的解析式为，①
将①式配方，得，
所以顶点P的坐标为（4，﹣2），
令y=0，得，
解得x1=2，x2=6．所以点B的坐标是（6，0）．

（2）在直线 y=x上存在点D，使四边形OPBD为平行四边形．
理由如下：
设直线PB的解析式为y=kx+b，把B（6，0），P（4，﹣2）分别代入，得
，
解得，
所以直线PB的解析式为．
又因为直线OD的解析式为，
所以直线PB∥OD．
设直线OP的解析式为y=mx，
把P（4，﹣2）代入，得，
解得．
如果OP∥BD，那么四边形OPBD为平行四边形．
设直线BD的解析式为，
将B（6，0）代入，得0=，
所以所以直线BD的解析式为，
解方程组，
得，
同样还存在第二种情况，如图所示，D′点和D关于原点对称，因此D′的坐标为（﹣2，﹣2），
所以D点的坐标为（2，2）或（﹣2，﹣2）．

（3）符合条件的点M存在．验证如下：
过点P作x轴的垂线，垂足为C，则PC=2，AC=2，
由勾股定理，可得AP=4，PB=4，又AB=4，
所以△APB是等边三角形，
只要作∠PAB的平分线交抛物线于M点，
连接PM，BM，由于AM=AM，∠PAM=∠BAM，AB=AP，
可得△AMP≌△AMB．
因此即存在这样的点M，使△AMP≌△AMB．
方法二：
（4）过点G作x轴垂线，垂足为H，
∵⊙G为△OBD的外接圆，
∴点G在线段OH的垂直平分线上，且GO=GD，
∵B（6，0），∴lGH：x=3，
设G点坐标为（3，m），O（0，0），D（2，2），
∴（3﹣0）2+（m﹣0）2=（3﹣2）2+（m﹣2）2，
∴m=，
∴G点的坐标为（3，）．


　
3．（2012•宜宾）如图，抛物线y=x2﹣2x+c的顶点A在直线l：y=x﹣5上．
（1）求抛物线顶点A的坐标；
（2）设抛物线与y轴交于点B，与x轴交于点C、D（C点在D点的左侧），试判断△ABD的形状；
（3）在直线l上是否存在一点P，使以点P、A、B、D为顶点的四边形是平行四边形？若存在，求点P的坐标；若不存在，请说明理由．

【解答】方法一：
解：（1）∵顶点A的横坐标为x=﹣=1，且顶点A在y=x﹣5上，
∴当x=1时，y=1﹣5=﹣4，
∴A（1，﹣4）．

（2）△ABD是直角三角形．
将A（1，﹣4）代入y=x2﹣2x+c，可得，1﹣2+c=﹣4，∴c=﹣3，
∴y=x2﹣2x﹣3，∴B（0，﹣3）
当y=0时，x2﹣2x﹣3=0，x1=﹣1，x2=3
∴C（﹣1，0），D（3，0），
BD2=OB2+OD2=18，AB2=（4﹣3）2+12=2，AD2=（3﹣1）2+42=20，
BD2+AB2=AD2，
∴∠ABD=90°，即△ABD是直角三角形．

（3）存在．
由题意知：直线y=x﹣5交y轴于点E（0，﹣5），交x轴于点F（5，0）
∴OE=OF=5，
又∵OB=OD=3
∴△OEF与△OBD都是等腰直角三角形
∴BD∥l，即PA∥BD
则构成平行四边形只能是PADB或PABD，如图，
过点P作y轴的垂线，过点A作x轴的垂线交过P且平行于x轴的直线于点G．
设P（x1，x1﹣5），则G（1，x1﹣5）
则PG=|1﹣x1|，AG=|5﹣x1﹣4|=|1﹣x1|
PA=BD=3
由勾股定理得：
（1﹣x1）2+（1﹣x1）2=18，x12﹣2x1﹣8=0，x1=﹣2或4
∴P（﹣2，﹣7）或P（4，﹣1），
存在点P（﹣2，﹣7）或P（4，﹣1）使以点A、B、D、P为顶点的四边形是平行四边形．
方法二：
（1）略．
（2）把A（1，﹣4）代入y=x2﹣2x+c，得c=3，
∴y=x2﹣2x+3=（x﹣3）（x+1），
∴D（3，0），B（0，﹣3），A（1，﹣4），
KBD==1，KAB==﹣1，
∴KBD•KAB=﹣1，
∴AB⊥BD，即△ABD为直角三角形．
（3）略．
（4）∵，解得：x1=1（舍），x2=2，
∴G（2，﹣3），
∵A（1，﹣4），B（0，﹣3），D（3，0），
∴GA==，
BD==3，
AB==，
∴S△BDG==4．


　
4．（2015•德州）已知抛物线y=﹣mx2+4x+2m与x轴交于点A（α，0），B（β，0），且=﹣2，
（1）求抛物线的解析式．
（2）抛物线的对称轴为l，与y轴的交点为C，顶点为D，点C关于l的对称点为E，是否存在x轴上的点M，y轴上的点N，使四边形DNME的周长最小？若存在，请画出图形（保留作图痕迹），并求出周长的最小值；若不存在，请说明理由．
（3）若点P在抛物线上，点Q在x轴上，当以点D、E、P、Q为顶点的四边形是平行四边形时，求点P的坐标．

【解答】解：（1）由题意可得：α，β是方程﹣mx2+4x+2m=0的两根，由根与系数的关系可得，
α+β=，αβ=﹣2，
∵=﹣2，
∴=﹣2，即=﹣2，
解得：m=1，
故抛物线解析式为：y=﹣x2+4x+2；

（2）存在x轴上的点M，y轴上的点N，使得四边形DNME的周长最小，
∵y=﹣x2+4x+2=﹣（x﹣2）2+6，
∴抛物线的对称轴l为x=2，顶点D的坐标为：（2，6），
又∵抛物线与y轴交点C的坐标为：（0，2），点E与点C关于l对称，
∴E点坐标为：（4，2），
作点D关于y轴的对称点D′，点E关于x轴的对称点E′，
则D′的坐标为；（﹣2，6），E′坐标为：（4，﹣2），
连接D′E′，交x轴于M，交y轴于N，
此时，四边形DNME的周长最小为：D′E′+DE，如图1所示：
延长E′E，′D交于一点F，在Rt△D′E′F中，D′F=6，E′F=8，
则D′E′===10，
设对称轴l与CE交于点G，在Rt△DGE中，DG=4，EG=2，
∴DE===2，
∴四边形DNME的周长最小值为：10+2；

（3）如图2，P为抛物线上的点，过点P作PH⊥x轴，垂足为H，
若以点D、E、P、Q为顶点的四边形为平行四边形，则△PHQ≌△DGE，
∴PH=DG=4，
∴|y|=4，
∴当y=4时，﹣x2+4x+2=4，
解得：x1=2+，x2=2﹣，
当y=﹣4时，﹣x2+4x+2=﹣4，
解得：x3=2+，x4=2﹣，
故P点的坐标为；（2﹣，4），（2+，4），（2﹣，﹣4），（2+，﹣4）．


　
5．（2015•绵阳）已知抛物线y=﹣x2﹣2x+a（a≠0）与y轴相交于A点，顶点为M，直线y=x﹣a分别与x轴、y轴相交于B，C两点，并且与直线MA相交于N点．
（1）若直线BC和抛物线有两个不同交点，求a的取值范围，并用a表示交点M，A的坐标；
（2）将△NAC沿着y轴翻转，若点N的对称点P恰好落在抛物线上，AP与抛物线的对称轴相交于点D，连接CD，求a的值及△PCD的面积；
（3）在抛物线y=﹣x2﹣2x+a（a＞0）上是否存在点P，使得以P，A，C，N为顶点的四边形是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．

【解答】解：（1）由题意得，，整理得2x2+5x﹣4a=0．
∵△=25+32a＞0，解得a＞﹣．
∵a≠0，
∴a＞﹣且a≠0．
令x=0，得y=a，
∴A（0，a）．
由y=﹣（x+1）2+1+a得，M（﹣1，1+a）．

（2）设直线MA的解析式为y=kx+b（k≠0），
∵A（0，a），M（﹣1，1+a），
∴，解得，
∴直线MA的解析式为y=﹣x+a，
联立得，，解得，
∴N（，﹣）．
∵点P是点N关于y轴的对称点，
∴P（﹣，﹣）．
代入y=﹣x2﹣2x+a得，﹣=﹣a2+a+a，解得a=或a=0（舍去）．
∴A（0，），C（0，﹣），M（﹣1，），|AC|=，
∴S△PCD=S△PAC﹣S△ADC=|AC|•|xp|﹣|AC|•|x0|
=••（3﹣1）
=；

（3）①当点P在y轴左侧时，
∵四边形APCN是平行四边形，
∴AC与PN互相平分，N（，﹣），
∴P（﹣，）；
代入y=﹣x2﹣2x+a得，=﹣a2+a+a，解得a=，
∴P1（﹣，）．
②当点P在y轴右侧时，
∵四边形ACPN是平行四边形，
∴NP∥AC且NP=AC，
∵N（，﹣），A（0，a），C（0，﹣a），
∴P（，﹣）．
代入y=﹣x2﹣2x+a得，﹣=﹣a2﹣a+a，解得a=，
∴P2（，﹣）．
综上所述，当点P1（﹣，）和P2（，﹣）时，A、C、P、N能构成平行四边形．

　
6．（2015•湖北）边长为2的正方形OABC在平面直角坐标系中的位置如图所示，点D是边OA的中点，连接CD，点E在第一象限，且DE⊥DC，DE=DC．以直线AB为对称轴的抛物线过C，E两点．
（1）求抛物线的解析式；
（2）点P从点C出发，沿射线CB每秒1个单位长度的速度运动，运动时间为t秒．过点P作PF⊥CD于点F，当t为何值时，以点P，F，D为顶点的三角形与△COD相似？
（3）点M为直线AB上一动点，点N为抛物线上一动点，是否存在点M，N，使得以点M，N，D，E为顶点的四边形是平行四边形？若存在，请直接写出满足条件的点的坐标；若不存在，请说明理由．

【解答】解：（1）方法一：
过点E作EG⊥x轴于G点．
∵四边形OABC是边长为2的正方形，D是OA的中点，
∴OA=OC=2，OD=1，∠AOC=∠DGE=90°．
∵∠CDE=90°，
∴∠ODC+∠GDE=90°．
∵∠ODC+∠OCD=90°，
∴∠OCD=∠GDE．
在△OCD和△GED中，
∴△ODC≌△GED （AAS），
∴EG=OD=1，DG=OC=2．
∴点E的坐标为（3，1）．
∵抛物线的对称轴为直线AB即直线x=2，
∴可设抛物线的解析式为y=a（x﹣2）2+k，
将C、E点的坐标代入解析式，得
．
解得，
抛物线的解析式为y=（x﹣2）2+；

方法二：
过点E作EG⊥x轴于G点．
DE⊥DC⇒∠CDO+∠EDH=90°，
EG⊥x轴⇒∠DEH+∠EDH=90°，
∴∠CDO=∠DEH，DC=DE，
∴△ODC≌△GED⇒DG=OC=2，EG=OD=1，
∴E（3，1），
∴9a+3b+2=0，
∵﹣=2，
抛物线的解析式为y=（x﹣2）2+；

（2）方法一：
①若△DFP∽△COD，则∠PDF=∠DCO，
∴PD∥OC，
∴∠PDO=∠OCP=∠AOC=90°，
∴四边形PDOC是矩形，
∴PC=OD=1，
∴t=1；
②若△PFD∽△COD，则∠DPF=∠DCO，=．
∴∠PCF=90°﹣∠DCO=90﹣∠DPF=∠PDF．
∴PC=PD，
∴DF=CD．
∵CD2=OD2+OC2=22+12=5，
∴CD=，
∴DF=．
∵=，
∴PC=PD=×=，
t=，
综上所述：t=1或t=时，以点P，F，D为顶点的三角形与△COD相似；
方法二：
过点F作x轴的垂线，分别交BC，OA于G，H，
PF⊥CD⇒∠PFG+∠DFH=90°，
GH⊥OA⇒∠FDH+∠DFH=90°，
∴∠PFG=∠FDH⇒△PFG∽△FDH⇒，
∵PF⊥CD⇒KPF×KCD=﹣1，
∴lCD：y=﹣2x+2，
∴F（m，﹣2m+2），P（t，2），
∴，
∴m=，
∴F（，﹣），
∴=，
∴以P，F，D为顶点的三角形与△COD相似，
①，∴，∴t=，
②，∴，∴t=1，
综上所述：t=1或t=时，以点P，F，D为顶点的三角形与△COD相似；
方法三：
若以P，F，D为顶点的三角形与△COD相似，
则∠OCD=∠PDF或∠ODC=∠PDF，
①∠OCD=∠PDF⇒PD∥OC，∴CP=OD=1，∴t=1，
②∠ODC=∠PDF，作OO′⊥CD交CD于H，
∴KOO′×KCD=﹣1，
∴lCD：y=﹣2x+2，
∴H（m，﹣2m+2），
∴﹣2×=﹣1，
∴m=，
∴H（，），
∵H为OO′中点，∴O′（，），
∴lO′D：y=，
令y=2，∴x=，
即P（，2），
∴t=．

（3）存在，
四边形MDEN是平行四边形时，M1（2，1），N1（4，2）；
四边形MNDE是平行四边形时，M2（2，3），N2（0，2）；
四边形NDME是平行四边形时，M3（2，），N3（2，）．


　
7．（2015•广安）如图，边长为1的正方形ABCD一边AD在x负半轴上，直线l：y=x+2经过点B（x，1）与x轴，y轴分别交于点H，F，抛物线y=﹣x2+bx+c．
（1）求A，D两点的坐标及抛物线经过A，D两点时的解析式；
（2）当抛物线的顶点E（m，n）在直线l上运动时，连接EA，ED，试求△EAD的面积S与m之间的函数解析式，并写出m的取值范围；
（3）设抛物线与y轴交于G点，当顶点E在直线l上运动时，以A，C，E，G为顶点的四边形能否成为平行四边形？若能，求出E点坐标；若不能，请说明理由．

【解答】解：（1）∵直线l：y=x+2经过点B（x，1），
∴1=x+2，解得x=﹣2，
∴B（﹣2，1），
∴A（﹣2，0），D（﹣3，0），
∵抛物线经过A，D两点，
∴，解得，
∴抛物线经过A，D两点时的解析式为y=﹣x2﹣5x﹣6；

（2）∵点E（m，n）在直线l上，
∴n=m+2，
∴S=×1×[±（m+2）]=±（m+1），
即S=m+1（m＞﹣4）或S=﹣m﹣1（m＜﹣4）；

（3）如图，若以A，C，E，G为顶点的四边形能成为平行四边形，则AC=EG，AC∥EG，
作EH∥y轴交过G点平行于x轴的直线相交于H，则EH⊥GH，△EHG≌△CDA，
∴GH=AD=1，
∴E的横坐标为±1，
∵点E在直线l上，
∴y=×（﹣1）+2=，或y=×1+2=
当AC为对角线时，有E和G的横坐标之和等于A和C的横坐标之和，故可求得E（﹣5，﹣1/2）
∴E（﹣1，）；（1，）或（﹣5，﹣1/2）；
由于E为抛物线的顶点，G为抛物线与y轴的交点，故将其坐标代入y=﹣x2+bx+c，
检验可知当E取（1，）或（﹣5，﹣1/2）时，与此时的A、C、E构成平行四边形的G点并不是y轴与抛物线的交点，
与前提相矛盾；
综上，满足题意的E的坐标为（﹣1，）．

　
8．（2012秋•义乌市校级期中）已知抛物线：
（1）求抛物线y1的顶点坐标．
（2）将抛物线y1向右平移2个单位，再向上平移1个单位，得到抛物线y2，求抛物线y2的解析式．
（3）如图，抛物线y2的顶点为P，x轴上有一动点M，在y1、y2这两条抛物线上是否存在点N，使O（原点）、P、M、N四点构成以OP为一边的平行四边形？若存在，求出N点的坐标；若不存在，请说明理由．

【解答】解：（1）依题意把抛物线：
y1=﹣x2+2x
=﹣（x2﹣4x）
=﹣[（x﹣2）2﹣4]
=﹣（x﹣2）2+2，
故抛物线y1的顶点坐标为：（2，2）；

（2）∵抛物线y1向右平移2个单位，再向上平移1个单位，得到y2=﹣（x﹣4）2+3，
整理得y2=﹣x2+4x﹣5；

（3）符合条件的N点存在．
如图：作PA⊥x轴于点A，NB⊥x轴于点B，
∴∠PAO=∠MBN=90°，
若四边形OPMN为符合条件的平行四边形，则OP∥MN，且OP=MN，
∴∠POA=∠BMN，
在△POA和△NMB中

∴△POA≌△NMB（AAS），
∴PA=BN，
∵点P的坐标为（4，3），
∴NB=PA=3，
∵点N在抛物线y1、y2上，且P点为y1、y2的最高点
∴符合条件的N点只能在x轴下方，
①点N在抛物线y1上，则有：﹣x2+2x=﹣3
解得：x1=2﹣，x2=2+，
②点N在抛物线y2上，则有：﹣（x﹣4）2+3=﹣3
解得：x3=4﹣2或x4=4+2
故符合条件的N点有四个：N1（2﹣，﹣3），N2（4﹣2，﹣3），N3（2+，﹣3），N4（4+2，﹣3）．

　
9．（2012•襄阳）如图，在矩形OABC中，AO=10，AB=8，沿直线CD折叠矩形OABC的一边BC，使点B落在OA边上的点E处．分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系，抛物线y=ax2+bx+c经过O，D，C三点．
（1）求AD的长及抛物线的解析式；
（2）一动点P从点E出发，沿EC以每秒2个单位长的速度向点C运动，同时动点Q从点C出发，沿CO以每秒1个单位长的速度向点O运动，当点P运动到点C时，两点同时停止运动．设运动时间为t秒，当t为何值时，以P、Q、C为顶点的三角形与△ADE相似？
（3）点N在抛物线对称轴上，点M在抛物线上，是否存在这样的点M与点N，使以M，N，C，E为顶点的四边形是平行四边形？若存在，请直接写出点M与点N的坐标（不写求解过程）；若不存在，请说明理由．

【解答】方法一：
解：（1）∵四边形ABCO为矩形，
∴∠OAB=∠AOC=∠B=90°，AB=CO=8，AO=BC=10．
由题意，△BDC≌△EDC．
∴∠B=∠DEC=90°，EC=BC=10，ED=BD．
由勾股定理易得EO=6．
∴AE=10﹣6=4，
设AD=x，则BD=ED=8﹣x，由勾股定理，得x2+42=（8﹣x）2，
解得，x=3，∴AD=3．
∵抛物线y=ax2+bx+c过点D（3，10），C（8，0），O（0，0）
∴，
解得
∴抛物线的解析式为：y=﹣x2+x．

（2）∵∠DEA+∠OEC=90°，∠OCE+∠OEC=90°，
∴∠DEA=∠OCE，
由（1）可得AD=3，AE=4，DE=5．
而CQ=t，EP=2t，∴PC=10﹣2t．
当∠PQC=∠DAE=90°，△ADE∽△QPC，
∴=，即=，
解得t=．
当∠QPC=∠DAE=90°，△ADE∽△PQC，
∴=，即=，
解得t=．
∴当t=或时，以P、Q、C为顶点的三角形与△ADE相似．

（3）假设存在符合条件的M、N点，分两种情况讨论：
①
EC为平行四边形的对角线，由于抛物线的对称轴经过EC中点，若四边形MENC是平行四边形，那么M点必为抛物线顶点；
则：M（4，）；而平行四边形的对角线互相平分，那么线段MN必被EC中点（4，3）平分，则N（4，﹣）；
②EC为平行四边形的边，则ECMN，设N（4，m），则M（4﹣8，m+6）或M（4+8，m﹣6）；
将M（﹣4，m+6）代入抛物线的解析式中，得：m=﹣38，此时 N（4，﹣38）、M（﹣4，﹣32）；
将M（12，m﹣6）代入抛物线的解析式中，得：m=﹣26，此时 N（4，﹣26）、M（12，﹣32）；
综上，存在符合条件的M、N点，且它们的坐标为：
①M1（﹣4，﹣32），N1（4，﹣38）；②M2（12，﹣32），N2（4，﹣26）；③M3（4，），N3（4，﹣）．
方法二：
（1）略．
（2）∵E（0，6），C（8，0），
∴lEC：y=﹣x+6，
∵，EP=2t，
∴Px=t，
∴P（t，﹣t+6），Q（8﹣t，0），
∵△PQC∽△ADE，且∠ECO=∠AED，
∴PQ⊥OC或PQ⊥PC．
当PQ⊥OC时，Px=Qx，即t=8﹣t，∴t1=，
当PQ⊥PC时，KPQ•KPC=﹣1，∴t2=．

（3）M，N，C，E为顶点的四边形是平行四边形．设N（4，t），C（8，0），E（0，6），
∴，
∴M1（4，6﹣t），同理M2（﹣4，t+6），M3（12，t﹣6），
∴﹣t，∴t=﹣，
﹣×（﹣4）2+（﹣4）=t+6，∴t=﹣38，
﹣×122+×12=t﹣6，∴t=﹣26，
综上，存在符合条件的M、N点，且它们的坐标为：
①M1（4，），N1（4，﹣）；②M2（12，﹣32），N2（4，﹣26）；
③M3（﹣4，﹣32），N3（4，﹣38）．


　
10．（2012•恩施州）如图，已知抛物线y=﹣x2+bx+c与一直线相交于A（﹣1，0），C（2，3）两点，与y轴交于点N．其顶点为D．
（1）抛物线及直线AC的函数关系式；
（2）设点M（3，m），求使MN+MD的值最小时m的值；
（3）若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EF∥BD交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由；
（4）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值．

【解答】解：（1）由抛物线y=﹣x2+bx+c过点A（﹣1，0）及C（2，3）得，
，
解得，
故抛物线为y=﹣x2+2x+3
又设直线为y=kx+n过点A（﹣1，0）及C（2，3）得
，
解得
故直线AC为y=x+1；

（2）如图1，作N点关于直线x=3的对称点N′，则N′（6，3），由（1）得D（1，4），
故直线DN′的函数关系式为y=﹣x+，
当M（3，m）在直线DN′上时，MN+MD的值最小，
则m=﹣×=；

（3）由（1）、（2）得D（1，4），B（1，2），
∵点E在直线AC上，
设E（x，x+1），
①如图2，当点E在线段AC上时，点F在点E上方，
则F（x，x+3），
∵F在抛物线上，
∴x+3=﹣x2+2x+3，
解得，x=0或x=1（舍去）
∴E（0，1）；
②当点E在线段AC（或CA）延长线上时，点F在点E下方，
则F（x，x﹣1）
由F在抛物线上
∴x﹣1=﹣x2+2x+3
解得x=或x=
∴E（，）或（，）
综上，满足条件的点E的坐标为（0，1）、（，）或（，）；

（4）方法一：如图3，过点P作PQ⊥x轴交AC于点Q，交x轴于点H；过点C作CG⊥x轴于点G，设Q（x，x+1），则P（x，﹣x2+2x+3）
∴PQ=（﹣x2+2x+3）﹣（x+1）
=﹣x2+x+2
又∵S△APC=S△APQ+S△CPQ
=PQ•AG
=（﹣x2+x+2）×3
=﹣（x﹣）2+
∴面积的最大值为．

方法二：过点P作PQ⊥x轴交AC于点Q，交x轴于点H；过点C作CG⊥x轴于点G，如图3，
设Q（x，x+1），则P（x，﹣x2+2x+3）
又∵S△APC=S△APH+S直角梯形PHGC﹣S△AGC
=（x+1）（﹣x2+2x+3）+（﹣x2+2x+3+3）（2﹣x）﹣×3×3
=﹣x2+x+3
=﹣（x﹣）2+
∴△APC的面积的最大值为．



　
11．（2014•赤峰）如图，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣1，0），B（3，0）两点，与y轴交于点C（0，﹣3）．

（1）求该抛物线的解析式及顶点M坐标；
（2）求△BCM面积与△ABC面积的比；
（3）若P是x轴上一个动点，过P作射线PQ∥AC交抛物线于点Q，随着P点的运动，在抛物线上是否存在这样的点Q，使以A，P，Q，C为顶点的四边形为平行四边形？若存在，请求出Q点坐标；若不存在，请说明理由．
【解答】方法一：
解：（1）设抛物线解析式为y=a（x+1）（x﹣3），
∵抛物线过点（0，﹣3），
∴﹣3=a（0+1）（0﹣3），
∴a=1，
∴抛物线解析式为y=（x+1）（x﹣3）=x2﹣2x﹣3，
∵y=x2﹣2x﹣3=（x﹣1）2﹣4，
∴M（1，﹣4）．

（2）如图1，连接BC、BM、CM，作MD⊥x轴于D，

∵S△BCM=S梯形OCMD+S△BMD﹣S△BOC
=•（3+4）•1+•2×4﹣•3•3
=+﹣=3
S△ABC=•AB•OC=•4•3=6，
∴S△BCM：S△ABC=3：6=1：2．

（3）存在，理由如下：
①如图2，当Q在x轴下方时，作QE⊥x轴于E，

∵四边形ACQP为平行四边形，
∴PQ平行且相等AC，
∴△PEQ≌△AOC，
∴EQ=OC=3，
∴﹣3=x2﹣2x﹣3，
解得 x=2或x=0（与C点重合，舍去），
∴Q（2，﹣3）．
②如图3，当Q在x轴上方时，作QF⊥x轴于F，

∵四边形ACPQ为平行四边形，
∴QP平行且相等AC，
∴△PFQ≌△AOC，
∴FQ=OC=3，
∴3=x2﹣2x﹣3，
解得 x=1+或x=1﹣，
∴Q（1+，3）或（1﹣，3）．
综上所述，Q点为（2，﹣3）或（1+，3）或（1﹣，3）
方法二：
（1）略．
（2）连接BC、BM、CM，作MD⊥x轴于D，交BC于H，
∵B（3，0），C（0，﹣3），
∴lBC：y=x﹣3，
当x=1时，y=﹣2，∴H（1，﹣2）
∴S△BCM=（3﹣0）（﹣2+4）=3，
∵S△ABC=AB×OC=×3×4=6，
∴S△BCM：S△ABC=3：6=1：2，

（3）∵PQ∥AC，
∴当PQ=AC时，A、P、Q、C为顶点的四边形为平行四边形，即|QY|=|CY|，
设Q（t，t2﹣2t﹣3），
∴|t2﹣2t﹣3|=3，
①t2﹣2t﹣3=3，解得：t1=1+，t2=1﹣，
②t2﹣2t﹣3=﹣3，解得：t1=0（舍），t2=2，
综上所述，Q点为（2，﹣3）或（1+，3）或（1﹣，3）．

　
12．（2014•潍坊）如图，抛物线y=ax2+bx+c（a≠0）与y轴交于点C（0，4），与x轴交于点A和点B，其中点A的坐标为（﹣2，0），抛物线的对称轴x=1与抛物线交于点D，与直线BC交于点E．
（1）求抛物线的解析式；
（2）若点F是直线BC上方的抛物线上的一个动点，是否存在点F使四边形ABFC的面积为17，若存在，求出点F的坐标；若不存在，请说明理由；
（3）平行于DE的一条动直线l与直线BC相交于点P，与抛物线相交于点Q，若以D、E、P、Q为顶点的四边形是平行四边形，求点P的坐标．

【解答】方法一：
解：（1）∵抛物线y=ax2+bx+c（a≠0）过点C（0，4），
∴c=4 ①．
∵对称轴x=﹣=1，
∴b=﹣2a ②．
∵抛物线过点A（﹣2，0），
∴0=4a﹣2b+c ③，
由①②③解得，a=﹣，b=1，c=4，
∴抛物线的解析式为y=﹣x2+x+4；

（2）假设存在满足条件的点F，如图所示，连结BF、CF、OF，过点F作FH⊥x轴于点H，FG⊥y轴于点G．
设点F的坐标为（t，﹣t2+t+4），其中0＜t＜4，
则FH=﹣t2+t+4，FG=t，
∴S△OBF=OB•FH=×4×（﹣t2+t+4）=﹣t2+2t+8，
S△OFC=OC•FG=×4×t=2t，
∴S四边形ABFC=S△AOC+S△OBF+S△OFC=4﹣t2+2t+8+2t=﹣t2+4t+12．
令﹣t2+4t+12=17，
即t2﹣4t+5=0，
则△=（﹣4）2﹣4×5=﹣4＜0，
∴方程t2﹣4t+5=0无解，
故不存在满足条件的点F；

（3）设直线BC的解析式为y=kx+n（k≠0），
∵B（4，0），C（0，4），
∴，
解得，
∴直线BC的解析式为y=﹣x+4．
由y=﹣x2+x+4=﹣（x﹣1）2+，
∴顶点D（1，），
又点E在直线BC上，则点E（1，3），
于是DE=﹣3=．
若以D、E、P、Q为顶点的四边形是平行四边形，因为DE∥PQ，只须DE=PQ，
设点P的坐标是（m，﹣m+4），则点Q的坐标是（m，﹣m2+m+4）．
①当0＜m＜4时，PQ=（﹣m2+m+4）﹣（﹣m+4）=﹣m2+2m，
由﹣m2+2m=，
解得：m=1或3．
当m=1时，线段PQ与DE重合，m=1舍去，
∴m=3，P1（3，1）．
②当m＜0或m＞4时，PQ=（﹣m+4）﹣（﹣m2+m+4）=m2﹣2m，
由m2﹣2m=，
解得m=2±，经检验适合题意，
此时P2（2+，2﹣），P3（2﹣，2+）．
综上所述，满足题意的点P有三个，分别是P1（3，1），P2（2+，2﹣），P3（2﹣，2+）．
方法二：
（1）略．
（2）∵B（4，0），C（0，4），
∴lBC：y=﹣x+4，
过F点作x轴垂线，交BC于H，设F（t，﹣t2+t+4），
∴H（t，﹣t+4），
∵S四边形ABFC=S△ABC+S△BCF=17，
∴（4+2）×4+（﹣t2+t+4+t﹣4）×4=17，
∴t2﹣4t+5=0，
∴△=（﹣4）2﹣4×5＜0，
∴方程t2﹣4t+5=0无解，故不存在满足条件的点F．

（3）∵DE∥PQ，
∴当DE=PQ时，以D、E、P、Q为顶点的四边形是平行四边形，
∵y=﹣x2+x+4，
∴D（1，），
∵lBC：y=﹣x+4，
∴E（1，3），
∴DE=﹣3=，
设点F的坐标是（m，﹣m+4），则点Q的坐标是（m，﹣m2+m+4），
∴|﹣m+4+m2﹣m﹣4|=，
∴m2﹣2m=或m2﹣2m=﹣，
∴m=1，m=3，m=2+，m=2﹣，
经检验，当m=1时，线段PQ与DE重合，故舍去．
∴P1（3，1），P2（2+，2﹣），P3（2﹣，2+）．



　
13．（2014•济宁）如图，抛物线y=x2+bx+c与x轴交于A（5，0）、B（﹣1，0）两点，过点A作直线AC⊥x轴，交直线y=2x于点C；
（1）求该抛物线的解析式；
（2）求点A关于直线y=2x的对称点A′的坐标，判定点A′是否在抛物线上，并说明理由；
（3）点P是抛物线上一动点，过点P作y轴的平行线，交线段CA′于点M，是否存在这样的点P，使四边形PACM是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．

【解答】方法一：
解：（1）∵y=x2+bx+c与x轴交于A（5，0）、B（﹣1，0）两点，
∴，
解得．
∴抛物线的解析式为y=x2﹣x﹣．

（2）如答图所示，过点A′作A′E⊥x轴于E，AA′与OC交于点D，
∵点C在直线y=2x上，
∴C（5，10）
∵点A和A′关于直线y=2x对称，
∴OC⊥AA′，A′D=AD．
∵OA=5，AC=10，
∴OC===．
∵S△OAC=OC•AD=OA•AC，
∴AD=．
∴AA′=，
在Rt△A′EA和Rt△OAC中，
∵∠A′AE+∠A′AC=90°，
∠ACD+∠A′AC=90°，
∴∠A′AE=∠ACD．
又∵∠A′EA=∠OAC=90°，
∴Rt△A′EA∽Rt△OAC．
∴，
即．
∴A′E=4，AE=8．
∴OE=AE﹣OA=3．
∴点A′的坐标为（﹣3，4），
当x=﹣3时，
y=×（﹣3）2+3﹣=4．
所以，点A′在该抛物线上．

（3）存在．
理由：设直线CA′的解析式为y=kx+b，
则，
解得
∴直线CA′的解析式为y=x+
设点P的坐标为（x，x2﹣x﹣），则点M为（x，x+）．
∵PM∥AC，
∴要使四边形PACM是平行四边形，只需PM=AC．又点M在点P的上方，
∴（x+）﹣（x2﹣x﹣）=10．
解得x1=2，x2=5（不合题意，舍去）
当x=2时，y=﹣．
∴当点P运动到（2，﹣）时，四边形PACM是平行四边形．
方法二：
（1）略．
（2）设AA′与直线OC的交点为H，
∵点A，点A′关于直线OC：y=2x对称，
∴AA′⊥OC，KOC•KAA′=﹣1，
∵KOC=2，∴KAA′=﹣，
∵A（5，0），
∴lAA′：y=﹣x+，lOC：y=2x，
∴H（1，2），
∵H为AA′的中点，
∴⇒，
∴A′X=﹣3，A′Y=4，
∴A′（﹣3，4），
当x=﹣3时，y=×（﹣3）2+3﹣=4，
∴点A在抛物线上．

（3）∵PM∥AC，要使四边形PACM是平行四边形，只需PM=AC，
∵直线AC⊥x轴，∴Cx=Ax，
∵A（5，0），
∴Cx=5，
∵lOC：y=2x，
∴CY=10，
∴C（5，10），
∵A′（﹣3，4），
∴lCA′：y=x+，
∵M在线段CA′上，点M在点P的上方，
∴设M（t，），
∴P（t，t2﹣t﹣），
∴﹣（t2﹣t﹣）=10，
∴t1=2，t2=5（舍），
∴P（2，﹣）．


　
14．（2014•东营）如图，直线y=2x+2与x轴交于点A，与y轴交于点B，把△AOB沿y轴翻折，点A落到点C，过点B的抛物线y=﹣x2+bx+c与直线BC交于点D（3，﹣4）．
（1）求直线BD和抛物线的解析式；
（2）在第一象限内的抛物线上，是否存在一点M，作MN垂直于x轴，垂足为点N，使得以M、O、N为顶点的三角形与△BOC相似？若存在，求出点M的坐标；若不存在，请说明理由；
（3）在直线BD上方的抛物线上有一动点P，过点P作PH垂直于x轴，交直线BD于点H，当四边形BOHP是平行四边形时，试求动点P的坐标．

【解答】方法一：
解：（1）∵y=2x+2，
∴当x=0时，y=2，
∴B（0，2）．
当y=0时，x=﹣1，
∴A（﹣1，0）．
∵抛物线y=﹣x2+bx+c过点B（0，2），D（3，﹣4），
∴
解得：，
∴y=﹣x2+x+2；
设直线BD的解析式为y=kx+b，由题意，得
，
解得：，
∴直线BD的解析式为：y=﹣2x+2；

（2）存在．
如图1，设M（a，﹣a2+a+2）．
∵MN垂直于x轴，
∴MN=﹣a2+a+2，ON=a．
∵y=﹣2x+2，
∴y=0时，x=1，
∴C（1，0），
∴OC=1．
∵B（0，2），
∴OB=2．
当△BOC∽△MNO时，
∴，
∴，
解得：a1=1，a2=﹣2（舍去）
∴M（1，2）；
如图2，当△BOC∽△ONM时，
，
∴，
∴a=或（舍去），
∴M（，）．
∴符合条件的点M的坐标为（1，2），（，）；

（3）设P（b，﹣b2+b+2），H（b，﹣2b+2）．
如图3，∵四边形BOHP是平行四边形，
∴BO=PH=2．
∵PH=﹣b2+b+2+2b﹣2=﹣b2+3b．
∴2=﹣b2+3b
∴b1=1，b2=2．
当b=1时，P（1，2），
当b=2时，P（2，0）
∴P点的坐标为（1，2）或（2，0）．

方法二：
（1）略．
（2）设M（a，﹣a2+a+2），
∵MN⊥x轴，
∴∠OMN=∠OBA或∠OMN=∠OAB，
①当∠OMN=∠OBA时，
∵△BOC∽△MON，
∴，
∴，
∴a1=1，a2=﹣2（舍），
∴M1（1，2），
②当∠OMN=∠OAB时，
∵△BOC∽△MON，
∴OM⊥BC，
∴KOM×KBC=﹣1，
∴=﹣1，
∴2a2﹣a﹣4=0，
∴a1=，a2=（舍），
∴M2（，）．

（3）设P（b，﹣b2+b+2），H（b，﹣2b+2），
∵四边形BOHP是平行四边形，
∴BO=PH=2，
∵PH=﹣b2+b+2+2b﹣2=﹣b2+3b．
∴2=﹣b2+3b，
∴b1=1，b2=2，
当b=1时，P（1，2），
当b=2时，P（2，0），
∴P点的坐标为（1，2）或（2，0）．



　
15．（2014•山西）综合与探究：如图，在平面直角坐标系xOy中，四边形OABC是平行四边形，A、C两点的坐标分别为（4，0），（﹣2，3），抛物线W经过O、A、C三点，D是抛物线W的顶点．
（1）求抛物线W的解析式及顶点D的坐标；
（2）将抛物线W和▱OABC一起先向右平移4个单位后，再向下平移m（0＜m＜3）个单位，得到抛物线W′和▱O′A′B′C′，在向下平移的过程中，设▱O′A′B′C′与▱OABC的重叠部分的面积为S，试探究：当m为何值时S有最大值，并求出S的最大值；
（3）在（2）的条件下，当S取最大值时，设此时抛物线W′的顶点为F，若点M是x轴上的动点，点N是抛物线W′上的动点，试判断是否存在这样的点M和点N，使得以D、F、M、N为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．

【解答】方法一：
解：（1）设抛物线W的解析式为W=ax2+bx+c，
∵抛物线W经过O（0，0）、A（4，0）、C（﹣2，3）三点，
∴，
解得：
∴抛物线W的解析式为W=x2﹣x．
∵W=x2﹣x=（x﹣2）2﹣1，
∴顶点D的坐标为（2，﹣1）．

（2）由▱OABC得，CB∥OA，CB=OA=4．
又∵C点坐标为（﹣2，3），
∴B点的坐标为（2，3）．
如答图2，过点B作BE⊥x轴于点E，由平移可知，点C′在BE上，且BC′=m．

∴BE=3，OE=2，∴EA=OA﹣OE=2．
∵C′B′∥x轴，
∴△BC′G∽△BEA，
∴，即，
∴C′G=m．
由平移知，▱O′A′B′C′与▱OABC的重叠部分四边形C′HAG是平行四边形．
∴S=C′G•C′E=m（3﹣m）=﹣（m﹣）2+，
∴当m=时，S有最大值为．

（3）答：存在．
在（2）的条件下，抛物线W向右平移4个单位，再向下平移个单位，得到抛物线W′，
∵D（2，﹣1），∴F（6，﹣）；
∴抛物线W′的解析式为：y=（x﹣6）2﹣．
设M（t，0），
以D、F、M、N为顶点的四边形是平行四边形，
①若点N在x轴下方，如答图3所示：

过点D作DP∥y轴，过点F作FP⊥DP于点P，
∵D（2，﹣1），F（6，﹣），∴DP=，FP=4；
过点N作NQ⊥x轴于点Q，
由四边形FDMN为平行四边形，易证△DFP≌△NMQ，
∴MQ=FP=4，NQ=DP=，
∴N（4+t，﹣），
将点N坐标代入抛物线W′的解析式y=（x﹣6）2﹣，得：（t﹣2）2﹣=﹣，
解得：t=0或t=4，
∴点M的坐标为（0，0）或（4，0）；
②若点N在x轴上方，（请自行作图）
与①同理，得N（t﹣4，）
将点N坐标代入抛物线W′的解析式y=（x﹣6）2﹣，得：（t﹣10）2﹣=，
解得：t=6或t=14，
∴点M的坐标为（6，0）或（14，0）．
综上所述，存在这样的点M和点N，点M的坐标分别为（0，0），（4，0），（6，0），（14，0）．
方法二：
（1）略．
（2）∵抛物线W和▱OABC一起向右平移4个单位后，再向下平移m个单位．
∴O′（4，﹣m），C′（2，3﹣m），
设lO′C′：y=kx+b，
∴⇒，
∴lO′C′：y=﹣x+6﹣m，
∴当y=0时，x=，
∴H（，0），
∵A（4，0），C′（2，3﹣m），
∴S=C′y×（Ax﹣Hx）=（3﹣m）（4﹣）=﹣m2+2m，
∴当m=时，S最大值为．

（3）∵D（2，﹣1），当m=时，F（6，﹣），
∵D、M、F、N为顶点的四边形是平行四边形，
∴，
∴，
∴N1（t+4，﹣），同理N2（t﹣4，），N3（8﹣t，﹣）．
∴①（t+4﹣6）2﹣=﹣，∴t1=0，t2=4，
②（t﹣4﹣6）2﹣=，∴t1=6，t2=14，
③（8﹣t﹣6）2﹣=﹣，∴无解，
综上所述，存在这样的点M和点N，点M的坐标分别为（0，0），（4，0），（6，0），（14，0）．
　
16．（2016•南充）如图，抛物线与x轴交于点A（﹣5，0）和点B（3，0）．与y轴交于点C（0，5）．有一宽度为1，长度足够的矩形（阴影部分）沿x轴方向平移，与y轴平行的一组对边交抛物线于点P和Q，交直线AC于点M和N．交x轴于点E和F．
（1）求抛物线的解析式；
（2）当点M和N都在线段AC上时，连接MF，如果sin∠AMF=，求点Q的坐标；
（3）在矩形的平移过程中，当以点P，Q，M，N为顶点的四边形是平行四边形时，求点M的坐标．

【解答】解：（1）∵抛物线与x轴交于点A（﹣5，0），B（3，0），
∴可以假设抛物线为y=a（x+5）（x﹣3），把点（0，5）代入得到a=﹣，
∴抛物线的解析式为y=﹣x2﹣x+5．
（2）作FG⊥AC于G，设点F坐标（m，0），
则AF=m+5，AE=EM=m+6，FG=（m+5），FM==，
∵sin∠AMF=，
∴=，
∴=，整理得到2m2+19m+44=0，
∴（m+4）（2m+11）=0，
∴m=﹣4或﹣5.5（舍弃），
∴点Q坐标（﹣4，）．
（3）①当MN是对角线时，设点F（m，0）．
∵直线AC解析式为y=x+5，
∴点N（m，m+5），点M（m+1，m+6），
∵QN=PM，
∴﹣m2﹣m+5﹣m﹣5=m+6﹣[﹣（m+1）2﹣（m+1）+5]，
解得m=﹣3±，
∴点M坐标（﹣2+，3+）或（﹣2﹣，3﹣）．
②当MN为边时，MN=PQ=，设点Q（m，﹣m2﹣m+5）则点P（m+1，﹣m2﹣m+6），
∴﹣m2﹣m+6=﹣（m+1）2﹣（m+1）+5，
解得m=﹣3．
∴点M坐标（﹣2，3），
综上所述以点P，Q，M，N为顶点的四边形是平行四边形时，点M的坐标为（﹣2，3）或（﹣2+，3+）或（﹣2﹣，3﹣）．

　
17．（2016•成都）如图，在平面直角坐标系xOy中，抛物线y=a（x+1）2﹣3与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C（0，﹣），顶点为D，对称轴与x轴交于点H，过点H的直线l交抛物线于P，Q两点，点Q在y轴的右侧．
（1）求a的值及点A，B的坐标；
（2）当直线l将四边形ABCD分为面积比为3：7的两部分时，求直线l的函数表达式；
（3）当点P位于第二象限时，设PQ的中点为M，点N在抛物线上，则以DP为对角线的四边形DMPN能否为菱形？若能，求出点N的坐标；若不能，请说明理由．

【解答】解：（1）∵抛物线与y轴交于点C（0，﹣）．
∴a﹣3=﹣，解得：a=，
∴y=（x+1）2﹣3
当y=0时，有（x+1）2﹣3=0，
∴x1=2，x2=﹣4，
∴A（﹣4，0），B（2，0）．
（2）∵A（﹣4，0），B（2，0），C（0，﹣），D（﹣1，﹣3）
∴S四边形ABCD=S△ADH+S梯形OCDH+S△BOC=×3×3+（+3）×1+×2×=10．
从面积分析知，直线l只能与边AD或BC相交，所以有两种情况：
①当直线l边AD相交与点M1时，则S=×10=3，
∴×3×（﹣y）=3
∴y=﹣2，点M1（﹣2，﹣2），过点H（﹣1，0）和M1（﹣2，﹣2）的直线l的解析式为y=2x+2．
②当直线l边BC相交与点M2时，同理可得点M2（，﹣2），过点H（﹣1，0）和M2（，﹣2）的直线l的解析式为y=﹣x﹣．
综上所述：直线l的函数表达式为y=2x+2或y=﹣x﹣．
（3）设P（x1，y1）、Q（x2，y2）且过点H（﹣1，0）的直线PQ的解析式为y=kx+b，
∴﹣k+b=0，
∴b=k，
∴y=kx+k．
由，
∴+（﹣k）x﹣﹣k=0，
∴x1+x2=﹣2+3k，y1+y2=kx1+k+kx2+k=3k2，
∵点M是线段PQ的中点，∴由中点坐标公式的点M（k﹣1，k2）．
假设存在这样的N点如图，直线DN∥PQ，设直线DN的解析式为y=kx+k﹣3
由，解得：x1=﹣1，x2=3k﹣1，∴N（3k﹣1，3k2﹣3）
∵四边形DMPN是菱形，
∴DN=DM，
∴（3k）2+（3k2）2=（）2+（）2，
整理得：3k4﹣k2﹣4=0，
∵k2+1＞0，
∴3k2﹣4=0，
解得k=±，
∵k＜0，
∴k=﹣，
∴P（﹣3﹣1，6），M（﹣﹣1，2），N（﹣2﹣1，1）
∴PM=DN=2，
∵PM∥DN，
∴四边形DMPN是平行四边形，
∵DM=DN，
∴四边形DMPN为菱形，
∴以DP为对角线的四边形DMPN能成为菱形，此时点N的坐标为（﹣2﹣1，1）．