

2020年贵州省铜仁市中考数学试卷(解析版)
展开一.选择题(共10小题)
1.﹣3的绝对值是( )
A.﹣3 B.3 C. D.﹣
2.我国高铁通车总里程居世界第一,预计到2020年底,高铁总里程大约39000千米,39000用科学记数法表示为( )
A.39×103 B.3.9×104 C.3.9×10﹣4 D.39×10﹣3
3.如图,直线AB∥CD,∠3=70°,则∠1=( )
A.70° B.100° C.110° D.120°
4.一组数据4,10,12,14,则这组数据的平均数是( )
A.9 B.10 C.11 D.12
5.已知△FHB∽△EAD,它们的周长分别为30和15,且FH=6,则EA的长为( )
A.3 B.2 C.4 D.5
6.实数a,b在数轴上对应的点的位置如图所示,下列结论正确的是( )
A.a>b B.﹣a<b C.a>﹣b D.﹣a>b
7.已知等边三角形一边上的高为2,则它的边长为( )
A.2 B.3 C.4 D.4
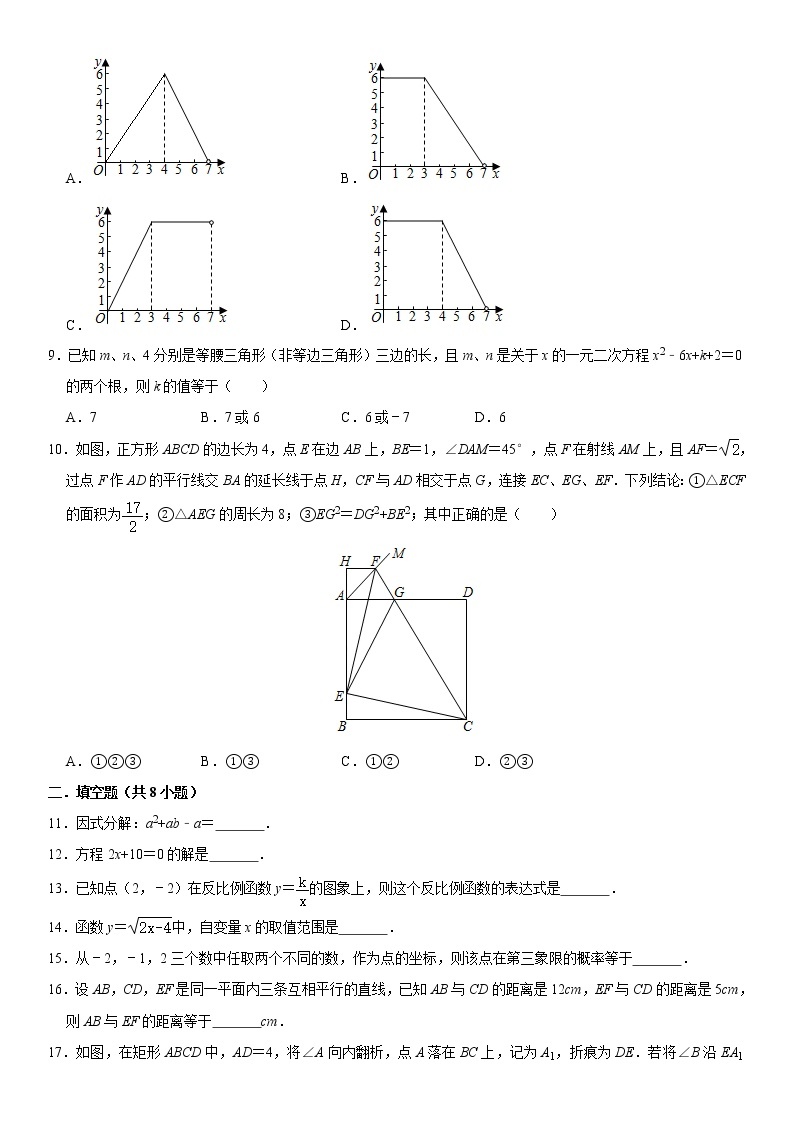
8.如图,在矩形ABCD中,AB=3,BC=4,动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是( )
A. B.
C. D.
9.已知m、n、4分别是等腰三角形(非等边三角形)三边的长,且m、n是关于x的一元二次方程x2﹣6x+k+2=0的两个根,则k的值等于( )
A.7 B.7或6 C.6或﹣7 D.6
10.如图,正方形ABCD的边长为4,点E在边AB上,BE=1,∠DAM=45°,点F在射线AM上,且AF=,过点F作AD的平行线交BA的延长线于点H,CF与AD相交于点G,连接EC、EG、EF.下列结论:①△ECF的面积为;②△AEG的周长为8;③EG2=DG2+BE2;其中正确的是( )
A.①②③ B.①③ C.①② D.②③
二.填空题(共8小题)
11.因式分解:a2+ab﹣a= .
12.方程2x+10=0的解是 .
13.已知点(2,﹣2)在反比例函数y=的图象上,则这个反比例函数的表达式是 .
14.函数y=中,自变量x的取值范围是 .
15.从﹣2,﹣1,2三个数中任取两个不同的数,作为点的坐标,则该点在第三象限的概率等于 .
16.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD的距离是5cm,则AB与EF的距离等于 cm.
17.如图,在矩形ABCD中,AD=4,将∠A向内翻析,点A落在BC上,记为A1,折痕为DE.若将∠B沿EA1向内翻折,点B恰好落在DE上,记为B1,则AB= .
18.观察下列等式:
2+22=23﹣2;
2+22+23=24﹣2;
2+22+23+24=25﹣2;
2+22+23+24+25=26﹣2;
…
已知按一定规律排列的一组数:220,221,222,223,224,…,238,239,240,若220=m,则220+221+222+223+224+…+238+239+240= (结果用含m的代数式表示).
三.解答题(共7小题)
19.(1)计算:2÷﹣(﹣1)2020﹣﹣(﹣)0.
(2)先化简,再求值:(a+)÷(),自选一个a值代入求值.
20.如图,∠B=∠E,BF=EC,AC∥DF.求证:△ABC≌△DEF.
21.某校计划组织学生参加学校书法、摄影、篮球、乒乓球四个课外兴趣小组,要求每人必须参加并且只能选择其中的一个小组,为了了解学生对四个课外小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把调查结果制成如图所示的两幅不完整的统计图,请你根据给出的信息解答下列问题:
(1)求该校参加这次问卷调查的学生人数,并补全条形统计图(画图后请标注相应的数据);
(2)m= ,n= ;
(3)若该校共有2000名学生,试估计该校选择“乒乓球”课外兴趣小组的学生有多少人?
22.如图,一艘船由西向东航行,在A处测得北偏东60°方向上有一座灯塔C,再向东继续航行60km到达B处,这时测得灯塔C在北偏东30°方向上,已知在灯塔C的周围47km内有暗礁,问这艘船继续向东航行是否安全?
23.某文体商店计划购进一批同种型号的篮球和同种型号的排球,每一个排球的进价是每一个篮球的进价的90%,用3600元购买排球的个数要比用3600元购买篮球的个数多10个.
(1)问每一个篮球、排球的进价各是多少元?
(2)该文体商店计划购进篮球和排球共100个,且排球个数不低于篮球个数的3倍,篮球的售价定为每一个100元,排球的售价定为每一个90元.若该批篮球、排球都能卖完,问该文体商店应购进篮球、排球各多少个才能获得最大利润?最大利润是多少?
24.如图,AB是⊙O的直径,C为⊙O上一点,连接AC,CE⊥AB于点E,D是直径AB延长线上一点,且∠BCE=∠BCD.
(1)求证:CD是⊙O的切线;
(2)若AD=8,=,求CD的长.
25.如图,已知抛物线y=ax2+bx+6经过两点A(﹣1,0),B(3,0),C是抛物线与y轴的交点.
(1)求抛物线的解析式;
(2)点P(m,n)在平面直角坐标系第一象限内的抛物线上运动,设△PBC的面积为S,求S关于m的函数表达式(指出自变量m的取值范围)和S的最大值;
(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N使得∠CMN=90°,且△CMN与△OBC相似,如果存在,请求出点M和点N的坐标.
2020年贵州省铜仁市中考数学试卷
参考答案与试题解析
一.选择题(共10小题)
1.﹣3的绝对值是( )
A.﹣3 B.3 C. D.﹣
【分析】直接利用绝对值的定义分析得出答案.
【解答】解:﹣3的绝对值是:3.
故选:B.
2.我国高铁通车总里程居世界第一,预计到2020年底,高铁总里程大约39000千米,39000用科学记数法表示为( )
A.39×103 B.3.9×104 C.3.9×10﹣4 D.39×10﹣3
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于39000有5位,所以可以确定n=5﹣1=4.
【解答】解:39000=3.9×104.
故选:B.
3.如图,直线AB∥CD,∠3=70°,则∠1=( )
A.70° B.100° C.110° D.120°
【分析】直接利用平行线的性质得出∠1=∠2,进而得出答案.
【解答】解:∵直线AB∥CD,
∴∠1=∠2,
∵∠3=70°,
∴∠1=∠2=180°﹣70°=110°.
故选:C.
4.一组数据4,10,12,14,则这组数据的平均数是( )
A.9 B.10 C.11 D.12
【分析】对于n个数x1,x2,…,xn,则=(x1+x2+…+xn)就叫做这n个数的算术平均数,据此列式计算可得.
【解答】解:这组数据的平均数为×(4+10+12+14)=10,
故选:B.
5.已知△FHB∽△EAD,它们的周长分别为30和15,且FH=6,则EA的长为( )
A.3 B.2 C.4 D.5
【分析】根据相似三角形的周长比等于相似比解答.
【解答】解:∵△FHB和△EAD的周长分别为30和15,
∴△FHB和△EAD的周长比为2:1,
∵△FHB∽△EAD,
∴=2,即=2,
解得,EA=3,
故选:A.
6.实数a,b在数轴上对应的点的位置如图所示,下列结论正确的是( )
A.a>b B.﹣a<b C.a>﹣b D.﹣a>b
【分析】根据数轴即可判断a和b的符号以及绝对值的大小,根据有理数的大小比较方法进行比较即可求解.
【解答】解:根据数轴可得:a<0,b>0,且|a|>|b|,
则a<b,﹣a>b,a<﹣b,﹣a>b.
故选:D.
7.已知等边三角形一边上的高为2,则它的边长为( )
A.2 B.3 C.4 D.4
【分析】根据等边三角形的性质:三线合一,利用勾股定理可求解即可.
【解答】解:根据等边三角形:三线合一,
设它的边长为x,可得:,
解得:x=4,x=﹣4(舍去),
故选:C.
8.如图,在矩形ABCD中,AB=3,BC=4,动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是( )
A. B.
C. D.
【分析】分别求出0≤x≤4、4<x<7时函数表达式,即可求解.
【解答】解:由题意当0≤x≤4时,
y=×AD×AB=×3×4=6,
当4<x<7时,
y=×PD×AD=×(7﹣x)×4=14﹣2x.
故选:D.
9.已知m、n、4分别是等腰三角形(非等边三角形)三边的长,且m、n是关于x的一元二次方程x2﹣6x+k+2=0的两个根,则k的值等于( )
A.7 B.7或6 C.6或﹣7 D.6
【分析】当m=4或n=4时,即x=4,代入方程即可得到结论,当m=n时,即△=(﹣6)2﹣4×(k+2)=0,解方程即可得到结论.
【解答】解:当m=4或n=4时,即x=4,
∴方程为42﹣6×4+k+2=0,
解得:k=6,
当m=n时,即△=(﹣6)2﹣4×(k+2)=0,
解得:k=7,
综上所述,k的值等于6或7,
故选:B.
10.如图,正方形ABCD的边长为4,点E在边AB上,BE=1,∠DAM=45°,点F在射线AM上,且AF=,过点F作AD的平行线交BA的延长线于点H,CF与AD相交于点G,连接EC、EG、EF.下列结论:①△ECF的面积为;②△AEG的周长为8;③EG2=DG2+BE2;其中正确的是( )
A.①②③ B.①③ C.①② D.②③
【分析】先判断出∠H=90°,进而求出AH=HF=1=BE.进而判断出△EHF≌△CBE(SAS),得出EF=EC,∠HEF=∠BCE,判断出△CEF是等腰直角三角形,再用勾股定理求出EC2=17,即可得出①正确;
先判断出四边形APFH是矩形,进而判断出矩形AHFP是正方形,得出AP=PH=AH=1,同理:四边形ABQP是矩形,得出PQ=4,BQ=1,FQ=5,CQ=3,再判断出△FPG∽△FQC,得出,求出PG=,再根据勾股定理求得EG=,即△AEG的周长为8,判断出②正确;
先求出DG=,进而求出DG2+BE2=,在求出EG2≠,判断出③错误,即可得出结论.
【解答】解:如图,在正方形ABCD中,AD∥BC,AB=BC=AD=4,∠B=∠BAD=90°,
∴∠HAD=90°,
∵HF∥AD,
∴∠H=90°,
∵∠HAF=90°﹣∠DAM=45°,
∴∠AFH=∠HAF.
∵AF=,
∴AH=HF=1=BE.
∴EH=AE+AH=AB﹣BE+AH=4=BC,
∴△EHF≌△CBE(SAS),
∴EF=EC,∠HEF=∠BCE,
∵∠BCE+∠BEC=90°,
∴HEF+∠BEC=90°,
∴∠FEC=90°,
∴△CEF是等腰直角三角形,
在Rt△CBE中,BE=1,BC=4,
∴EC2=BE2+BC2=17,
∴S△ECF=EF•EC=EC2=,故①正确;
过点F作FQ⊥BC于Q,交AD于P,
∴∠APF=90°=∠H=∠HAD,
∴四边形APFH是矩形,
∵AH=HF,
∴矩形AHFP是正方形,
∴AP=PH=AH=1,
同理:四边形ABQP是矩形,
∴PQ=AB=4,BQ=AP1,FQ=FP+PQ=5,CQ=BC﹣BQ=3,
∵AD∥BC,
∴△FPG∽△FQC,
∴,
∴,
∴PG=,
∴AG=AP+PG=,
在Rt△EAG中,根据勾股定理得,EG==,
∴△AEG的周长为AG+EG+AE=++3=8,故②正确;
∵AD=4,
∴DG=AD﹣AG=,
∴DG2+BE2=+1=,
∵EG2=()2=≠,
∴EG2≠DG2+BE2,故③错误,
∴正确的有①②,
故选:C.
二.填空题(共8小题)
11.因式分解:a2+ab﹣a= a(a+b﹣1) .
【分析】原式提取公因式即可.
【解答】解:原式=a(a+b﹣1).
故答案为:a(a+b﹣1).
12.方程2x+10=0的解是 x=﹣5 .
【分析】方程移项,把x系数化为1,即可求出解.
【解答】解:方程2x+10=0,
移项得:2x=﹣10,
解得:x=﹣5.
故答案为:x=﹣5.
13.已知点(2,﹣2)在反比例函数y=的图象上,则这个反比例函数的表达式是 y=﹣ .
【分析】把点(2,﹣2)代入反比例函数y=(k≠0)中求出k的值,从而得到反比例函数解析式.
【解答】解:∵反比例函数y=(k≠0)的图象上一点的坐标为(2,﹣2),
∴k=﹣2×2=﹣4,
∴反比例函数解析式为y=﹣,
故答案为:y=﹣.
14.函数y=中,自变量x的取值范围是 x≥2 .
【分析】因为当函数表达式是二次根式时,被开方数为非负数,所以2x﹣4≥0,可求x的范围.
【解答】解:2x﹣4≥0
解得x≥2.
15.从﹣2,﹣1,2三个数中任取两个不同的数,作为点的坐标,则该点在第三象限的概率等于 .
【分析】画树状图得出所有等可能结果,从中找到该点在第三象限的结果数,再利用概率公式求解可得.
【解答】解:画树状图如下
共有6种等可能情况,该点在第三象限的情况数有(﹣2,﹣1)和(﹣1,﹣2)这2种结果,
∴该点在第三象限的概率等于=,
故答案为:.
16.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD的距离是5cm,则AB与EF的距离等于 7或17 cm.
【分析】分两种情况讨论,EF在AB,CD之间或EF在AB,CD同侧,进而得出结论.
【解答】解:分两种情况:
①当EF在AB,CD之间时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12﹣5=7(cm).
②当EF在AB,CD同侧时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12+5=17(cm).
综上所述,EF与AB的距离为7cm或17cm.
故答案为:7或17.
17.如图,在矩形ABCD中,AD=4,将∠A向内翻析,点A落在BC上,记为A1,折痕为DE.若将∠B沿EA1向内翻折,点B恰好落在DE上,记为B1,则AB= .
【分析】依据△A1DB1≌△A1DC(AAS),即可得出A1C=A1B1,再根据折叠的性质,即可得到A1C=BC=2,最后依据勾股定理进行计算,即可得到CD的长,即AB的长.
【解答】解:由折叠可得,A1D=AD=4,∠A=∠EA1D=90°,∠BA1E=∠B1A1E,BA1=B1A1,∠B=∠A1B1E=90°,
∴∠EA1B1+∠DA1B1=90°=∠BA1E+∠CA1D,
∴∠DA1B1=∠CA1D,
又∵∠C=∠A1B1D,A1D=A1D,
∴△A1DB1≌△A1DC(AAS),
∴A1C=A1B1,
∴BA1=A1C=BC=2,
∴Rt△A1CD中,CD==,
∴AB=,
故答案为:.
18.观察下列等式:
2+22=23﹣2;
2+22+23=24﹣2;
2+22+23+24=25﹣2;
2+22+23+24+25=26﹣2;
…
已知按一定规律排列的一组数:220,221,222,223,224,…,238,239,240,若220=m,则220+221+222+223+224+…+238+239+240= m(2m﹣1) (结果用含m的代数式表示).
【分析】由题意可得220+221+222+223+224+…+238+239+240=220(1+2+22+…+219+220)=220(1+221﹣2)=220(220×2﹣1),再将220=m代入即可求解.
【解答】解:∵220=m,
∴220+221+222+223+224+…+238+239+240
=220(1+2+22+…+219+220)
=220(1+221﹣2)
=m(2m﹣1).
故答案为:m(2m﹣1).
三.解答题(共7小题)
19.(1)计算:2÷﹣(﹣1)2020﹣﹣(﹣)0.
(2)先化简,再求值:(a+)÷(),自选一个a值代入求值.
【分析】(1)原式利用除法法则,乘方的意义,算术平方根定义,以及零指数幂法则计算即可求出值;
(2)原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把a的值代入计算即可求出值.
【解答】解:(1)原式=2×2﹣1﹣2﹣1
=4﹣1﹣2﹣1
=0;
(2)原式=•
=•
=﹣,
当a=0时,原式=﹣3.
20.如图,∠B=∠E,BF=EC,AC∥DF.求证:△ABC≌△DEF.
【分析】首先利用平行线的性质得出∠ACB=∠DFE,进而利用全等三角形的判定定理ASA,进而得出答案.
【解答】证明:∵AC∥DF,
∴∠ACB=∠DFE,
∵BF=CE,
∴BC=EF,
在△ABC和△DEF中,,
∴△ABC≌△DEF(ASA).
21.某校计划组织学生参加学校书法、摄影、篮球、乒乓球四个课外兴趣小组,要求每人必须参加并且只能选择其中的一个小组,为了了解学生对四个课外小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把调查结果制成如图所示的两幅不完整的统计图,请你根据给出的信息解答下列问题:
(1)求该校参加这次问卷调查的学生人数,并补全条形统计图(画图后请标注相应的数据);
(2)m= 36 ,n= 16 ;
(3)若该校共有2000名学生,试估计该校选择“乒乓球”课外兴趣小组的学生有多少人?
【分析】(1)根据选择书法的学生人数和所占的百分比,可以求得该校参加这次问卷调查的学生人数,然后根据扇形统计图中选择篮球的占28%,即可求得选择篮球的学生人数,从而可以将条形统计图补充完整;
(2)根据条形统计图中的数据和(1)中的结果,可以得到m、n的值;
(3)根据统计图中的数据,可以计算出该校选择“乒乓球”课外兴趣小组的学生有多少人.
【解答】解:(1)该校参加这次问卷调查的学生有:20÷20%=100(人),
选择篮球的学生有:100×28%=28(人),
补全的条形统计图如右图所示;
(2)m%=×100%=36%,
n%=×100%=16%,
故答案为:36,16;
(3)2000×16%=320(人),
答:该校选择“乒乓球”课外兴趣小组的学生有320人.
22.如图,一艘船由西向东航行,在A处测得北偏东60°方向上有一座灯塔C,再向东继续航行60km到达B处,这时测得灯塔C在北偏东30°方向上,已知在灯塔C的周围47km内有暗礁,问这艘船继续向东航行是否安全?
【分析】过C作CD⊥AB于点D,根据方向角的定义及余角的性质求出∠BCA=30°,∠ACD=60°,证∠ACB=30°=∠BCA,根据等角对等边得出BC=AB=12,然后解Rt△BCD,求出CD即可.
【解答】解:过点C作CD⊥AB,垂足为D.如图所示:
根据题意可知∠BAC=90°﹣30°=30°,∠DBC=90°﹣30°=60°,
∵∠DBC=∠ACB+∠BAC,
∴∠BAC=30°=∠ACB,
∴BC=AB=60km,
在Rt△BCD中,∠CDB=90°,∠BDC=60°,sin∠BCD=,
∴sin60°=,
∴CD=60×sin60°=60×=30(km)>47km,
∴这艘船继续向东航行安全.
23.某文体商店计划购进一批同种型号的篮球和同种型号的排球,每一个排球的进价是每一个篮球的进价的90%,用3600元购买排球的个数要比用3600元购买篮球的个数多10个.
(1)问每一个篮球、排球的进价各是多少元?
(2)该文体商店计划购进篮球和排球共100个,且排球个数不低于篮球个数的3倍,篮球的售价定为每一个100元,排球的售价定为每一个90元.若该批篮球、排球都能卖完,问该文体商店应购进篮球、排球各多少个才能获得最大利润?最大利润是多少?
【分析】(1)设每一个篮球的进价是x元,则每一个排球的进价是90%x元,根据用3600元购买排球的个数要比用3600元购买篮球的个数多10个列出方程,解之即可得出结论;
(2)设文体商店计划购进篮球m个,总利润y元,根据题意用m表示y,结合m的取值范围和m为整数,即可得出获得最大利润的方案.
【解答】解:(1)设每一个篮球的进价是x元,则每一个排球的进价是90%x元,依题意有
+10=,
解得x=40,
经检验,x=40是原方程的解,
90%x=90%×40=36.
故每一个篮球的进价是40元,每一个排球的进价是36元;
(2)设文体商店计划购进篮球m个,总利润y元,则
y=(100﹣40)m+(90﹣36)(100﹣m)=6m+5400,
依题意有,
解得0<m≤25且m为整数,
∵m为整数,
∴y随m的增大而增大,
∴m=25时,y最大,这时y=6×25+5400=5550,
100﹣25=75(个).
故该文体商店应购进篮球25个、排球75个才能获得最大利润,最大利润是5550元.
24.如图,AB是⊙O的直径,C为⊙O上一点,连接AC,CE⊥AB于点E,D是直径AB延长线上一点,且∠BCE=∠BCD.
(1)求证:CD是⊙O的切线;
(2)若AD=8,=,求CD的长.
【分析】(1)连接OC,根据圆周角定理得到∠ACB=90°,根据余角的性质得到∠A=∠ECB,求得∠A=∠BCD,根据等腰三角形的性质得到∠A=∠ACO,等量代换得到∠ACO=∠BCD,求得∠DCO=90°,于是得到结论;
(2)设BC=k,AC=2k,根据相似三角形的性质即可得到结论.
【解答】(1)证明:连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵CE⊥AB,
∴∠CEB=90°,
∴∠ECB+∠ABC=∠ABC+∠CAB=90°,
∴∠A=∠ECB,
∵∠BCE=∠BCD,
∴∠A=∠BCD,
∵OC=OA,
∴∠A=∠ACO,
∴∠ACO=∠BCD,
∴∠ACO+∠BCO=∠BCO+∠BCD=90°,
∴∠DCO=90°,
∴CD是⊙O的切线;
(2)解:∵∠A=∠BCE,
∴tanA==tan∠BCE==,
设BC=k,AC=2k,
∵∠D=∠D,∠A=∠BCD,
∴△ACD∽△CBD,
∴==,
∵AD=8,
∴CD=4.
25.如图,已知抛物线y=ax2+bx+6经过两点A(﹣1,0),B(3,0),C是抛物线与y轴的交点.
(1)求抛物线的解析式;
(2)点P(m,n)在平面直角坐标系第一象限内的抛物线上运动,设△PBC的面积为S,求S关于m的函数表达式(指出自变量m的取值范围)和S的最大值;
(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N使得∠CMN=90°,且△CMN与△OBC相似,如果存在,请求出点M和点N的坐标.
【分析】(1)根据点A、B的坐标利用待定系数法即可求出抛物线的解析式;
(2)过点P作PF∥y轴,交BC于点F,利用二次函数图象上点的坐标特征可得出点C的坐标,根据点B、C的坐标利用待定系数法即可求出直线BC的解析式,设点P的坐标为(m,﹣2m2+4m+6),则点F的坐标为(m,﹣2m+6),进而可得出PF的长度,利用三角形的面积公式可得出S△PBC=﹣3m2+9m,配方后利用二次函数的性质即可求出△PBC面积的最大值;
(3)分两种不同情况,当点M位于点C上方或下方时,画出图形,由相似三角形的性质得出方程,求出点M,点N的坐标即可.
【解答】解:(1)将A(﹣1,0)、B(3,0)代入y=ax2+bx+6,
得:,解得:,
∴抛物线的解析式为y=﹣2x2+4x+6.
(2)过点P作PF∥y轴,交BC于点F,如图1所示.
当x=0时,y=﹣2x2+4x+6=6,
∴点C的坐标为(0,6).
设直线BC的解析式为y=kx+c,
将B(3,0)、C(0,6)代入y=kx+c,得:
,解得:,
∴直线BC的解析式为y=﹣2x+6.
设点P的坐标为(m,﹣2m2+4m+6),则点F的坐标为(m,﹣2m+6),
∴PF=﹣2m2+4m+6﹣(﹣2m+6)=﹣2m2+6m,
∴S△PBC=PF•OB=﹣3m2+9m=﹣3(m﹣)2+,
∴当m=时,△PBC面积取最大值,最大值为.
∵点P(m,n)在平面直角坐标系第一象限内的抛物线上运动,
∴0<m<3.
(3)存在点M、点N使得∠CMN=90°,且△CMN与△OBC相似.
如图2,∠CMN=90°,当点M位于点C上方,过点M作MD⊥y轴于点D,
∵∠CDM=∠CMN=90°,∠DCM=∠NCM,
∴△MCD∽△NCM,
若△CMN与△OBC相似,则△MCD与△NCM相似,
设M(a,﹣2a2+4a+6),C(0,6),
∴DC=﹣2a2+4a,DM=a,
当时,△COB∽△CDM∽△CMN,
∴,
解得,a=1,
∴M(1,8),
此时ND=DM=,
∴N(0,),
当时,△COB∽△MDC∽△NMC,
∴,
解得a=,
∴M(,),
此时N(0,).
如图3,当点M位于点C的下方,
过点M作ME⊥y轴于点E,
设M(a,﹣2a2+4a+6),C(0,6),
∴EC=2a2﹣4a,EM=a,
同理可得:或=2,△CMN与△OBC相似,
解得a=或a=3,
∴M(,)或M(3,0),
此时N点坐标为(0,)或(0,﹣).
综合以上得,M(1,8),N(0,)或M(,),N(0,)或M(,),N(0,)或M(3,0),N(0,﹣),使得∠CMN=90°,且△CMN与△OBC相似.








