



初中数学华师大版七年级下册9.2 多边形的内角和与外角和完美版课件ppt
展开预习P83-85 1.勾划出四边形、五边形、多边形、正多边形的概念 2.知道有几种方法将多边形分割成三角形 3.了解多边形的内角和公式
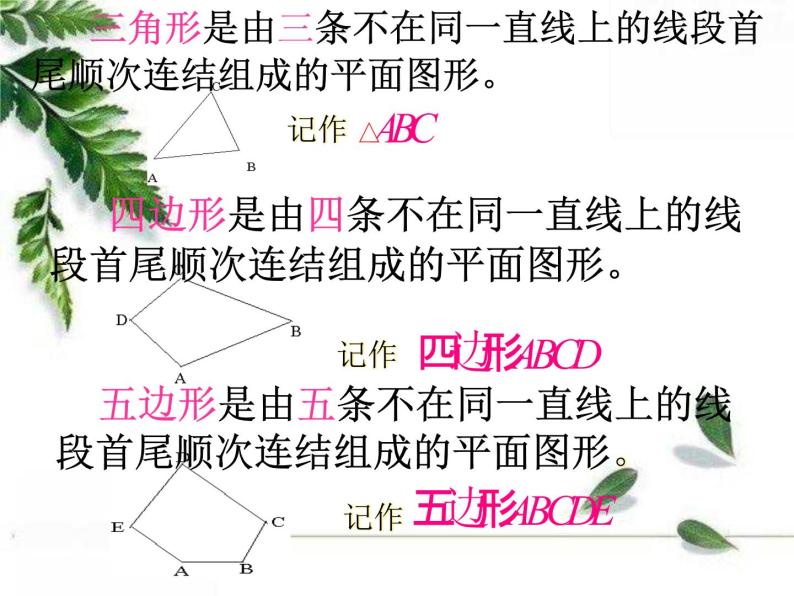
三角形是由三条不在同一直线上的线段首尾顺次连结组成的平面图形。
三角形的内角和定理是什么?外角和定理呢?
三角形是由三条不在同一直线上的线段首尾顺次连结组成的平面图形。
四边形是由四条不在同一直线上的线段首尾顺次连结组成的平面图形。
五边形是由五条不在同一直线上的线段首尾顺次连结组成的平面图形。
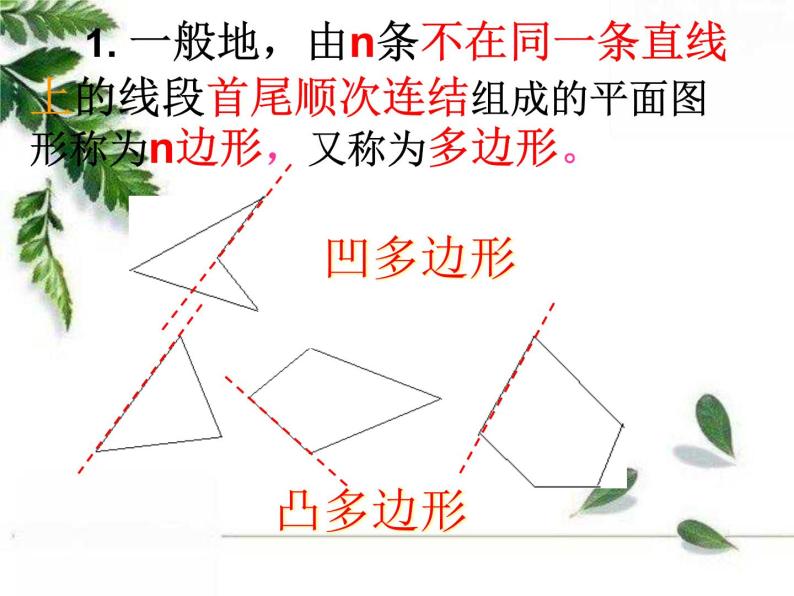
1. 一般地,由n条不在同一条直线上的线段首尾顺次连结组成的平面图形称为n边形,又称为多边形。
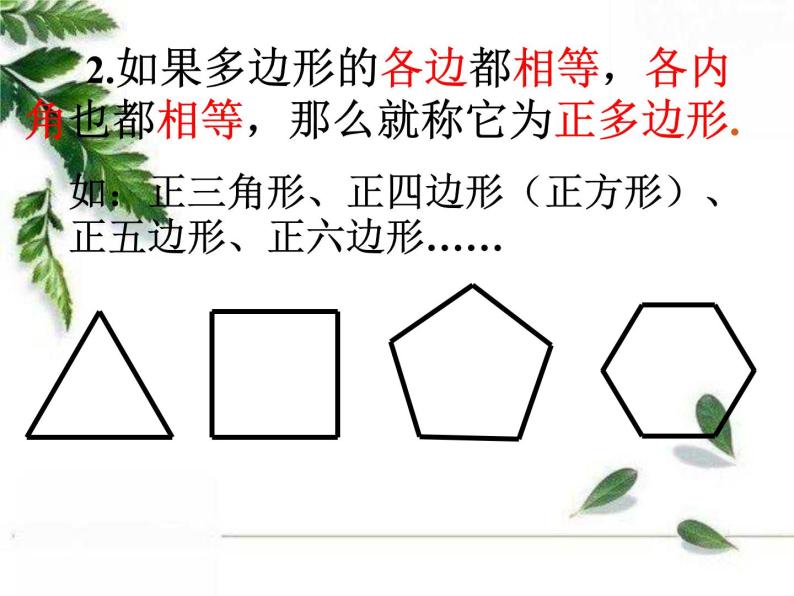
2.如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
如:正三角形、正四边形(正方形)、正五边形、正六边形……
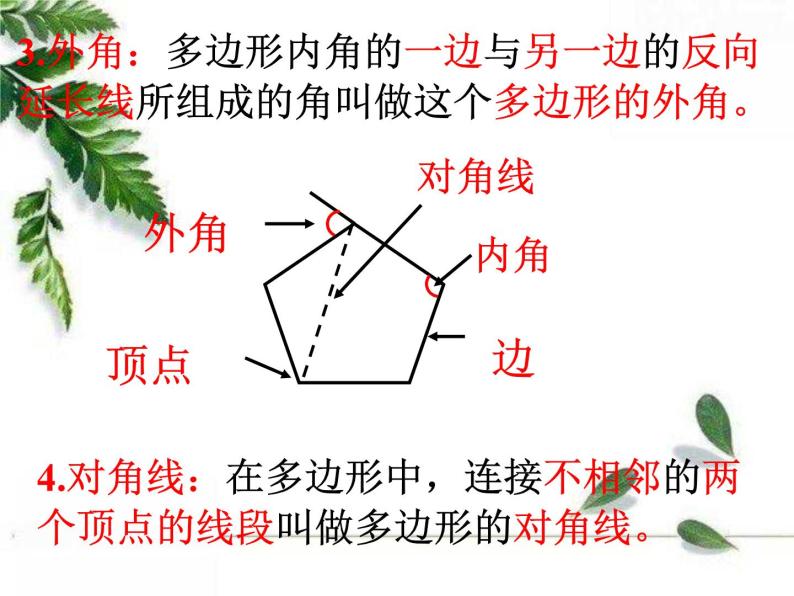
4.对角线:在多边形中,连接不相邻的两个顶点的线段叫做多边形的对角线。
3.外角:多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角。
问题 :五边形、六边形分别有多少个内角?多少个外角?
答:五边形有5个内角,10个(5对)外角; 六边形有6个内角,12个(6对)外角.
问题 :n边形有多少个内角?多少个外角?
答:n边形有n个内角,2n个(n对)外角.
回顾:把多边形分割成三角形的三种分法
从多边形的一个顶点出发可把这个多边形分成几个三角形?对角线多少条?
从多边形某边上的一点(不是顶点)可把这个多边形分成几个三角形?
从多边形上的内部一点出发可把这个多边形分成几个三角形?
请问:四边形从一个顶点出发,能引出几条对角线?
请问:五边形从一个顶点出发,能引出几条对角线?
请问:六边形从一个顶点出发,能引出几条对角线?
请问:n边形从一个顶点出发,能引出几条对角线?
五边形ABCDE从一个顶点出发可以引多少条对角线?共有几条对角线呢?
五边形ABCDE共有5条对角线。
从一个顶点出发可以引2条对角线
请大家思考:六边形ABCDEF共有几条对角线呢?
六边形ABCDEF共有9条对角线。
1.一个多边形共有27条对角线,那么这个多边形是 边形 。2.一个n边形的对角线恰好有n条,那么这个多边形是 边形。3.从多边形的一个顶点能引5条对角线,那么该多边形的边数为 。
问题3: 三角形、四边形、五边形…边形的内角和是多少呢?
n边形内角和定理:
把多边形划分成若干个三角形,再利用三角形的内角和为180º,求出多边形的内角和 .
仔细观察表格,回答问题:
1.多边形的边每增加1条,多边形的内角和增加 . 2.n边形的内角和为(n-2)·180º,说明 .
多边形的内角和是180º的整数倍
例1.求八边形的内角和。
求九边形的内角和。
例2.已知一个多边形的内角和等于2160º,求这个多边形的边数。
设这个多边形的边数为n,根据题意,得
已知一个多边形的内角和是2340º,则这个多边形是 边形 。
(n-2)·180º=2160º
∴这个多边形的边数是14.
1.一个五边形各个内角度数之比为2:3:4:5:6,则每个内角的度数分别为 。
解:设各内角的度数分别为2x,3x,4x,5x,6x
∴这个五边形各内角的度数分别为: 54º,81º,108º,135º,162º
完成P86 练习2题 (写清解题过程)
2.八边形与五边形的内角和之比为 。
解:八边形的内角和为:
∴ 1080 º:540º=2:1
3.已知两个多边形的内角和为1800º,且两个多边形的边数比为2:5,求这两个多边形的边数。
解:设这两个多边形的边数分别为2x,5x
∴ 这两个多边形的边数分别为4,10.
n边形和m边形的内角和的度数之差为720º,则n-m= 。
解:n边形的内角和为:
(n-2)-(m-2)=4
从与三角形的每个内角相邻的两个外角中分别取一个相加,得到的和,称为三角形的外角和。
从与多边形的每个内角相邻的两个外角中分别取一个相加,得到的和,称为多边形的外角和。
问题4:多边形的外角和是多少呢?
多边形的内角与外角的总和
任意多边形的外角和都为:
多边形的外角和与边数无关。
正n边形的每个内角的度数为:
正n边形的每个外角的度数为:
问题5.正n边形的内角的度数与外角的度数:
一个多边形的每个外角都是72º,这个多边形是几边形?内角和是多少?
解:设这个多边形的边数为n,
∴ 这个多边形是五边形。
∴ 这个多边形的内角和为:
(2)在一个多边形中,它的内角最多可以有几个是锐角?
(3)在一个多边形中,它的外角最多能有几个钝角?
(1)十边形的内角和是 ,外角和是 , 如果十边形的各个内角都相等,那么它的一个内角是 .
完成P88 练习第1、2题
1.一个多边形的每一个外角都等于45度,这个多边形是几边形?它的每一个内角是多少度? 2.在一个多边形中,它的内角最多可以有几个是锐角?
多边形外角和为360度,则外角中至多有三个钝角,因此多边形的内角最多可以有三个锐角。
1.一个正多边形的内角和为1440º,则它的一个外角的度数为 。2.若多边形的每一个内角为150º,则从它的一个顶点出发引出的对角线有 条。3.一个多边形的每一个内角都比与它相邻的外角的3倍还多20º,则这个多边形的内角和为 。
1. n边形的内角和定理是什么?
2.推导多边形内角和定理时所用的方法是什么?
3.多边形的外角和定理是什么?
4.多边形的内角与其相邻外角的和是多少?
6.多边形的内角与外角在计算中的相互转化。
把多边形划分成若干个三角形,再利用三角形的内角和为1800求出多边形的内角和.
5.多边形的对角线共有
[例]一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形, 则它的内角和是为
∴ 这个多边形是八边形.
(n2)×180°=3×360°
例:一个正多边形的一个内角比相邻外角大36°,求这个正多边形的边数.
解:设这个角的相邻的外角的度数为x, 则内角的度数为x+36° 根据题意,得 x+(x+36°)=180° 解得 x=72° ∴这个正多边形的边数为 : 360 °÷72°=5
1. 如果一个多边形的每一个内角都比它相邻的外角大100°,则这个多边形的边数为( )。
2. 一个多边形的外角最多有( )个是钝角.
3. 一个多边形的内角最多有( )个是锐角.
4. 内角和与外角和相等的多边形的边数是( ).
5.一个多边形每增加一条边,内角和增加( ). 外角和( ).
6.一个多边形裁去一个角(不过顶点)后,形成的多边形的外角和 ( ), 内角和( ).
正多边形的内角和与某一个外角的度数总和为1300°,求这个正多边形的边数
∵1300°÷180°
又∵多边形的内角和是180°的整数倍
∴ 这个外角的度数为40°
设这个正多边形的边数为n,则
一个多边形的内角和与其中一个外角的度数总和为1350°,求这个多边形的边数和这个外角的度数。
∵1350°÷180°
1.求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F的值
2.求∠A+ ∠B+ ∠C+ ∠D + ∠E+ ∠F + ∠G+ ∠H的值
3.求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F的值
4.求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F + ∠G的值
已知:∠1= ∠2= ∠3= ∠4=70º,求∠AED的度数。
已知:AB//CD,求∠1+ ∠2+ ∠3的度数。
问:在n边形内任取一点P,连结点P与多边形的每一个顶点,可得几个三角形?(P86 试一试---这个非常重要哟)
已知过m边形的一个顶点有7条对角线,n边形没有对角线,p边形有p条对角线,求 (m-p)n 的值.
解:∵过m边形的一个顶点有7条对角线 ∴ m-3=7 ∵n边形没有对角线 ∴ n-3=0 ∵p边形有p条对角线 ∴
完成P88 习题9.2 第1、2、3题
已知一个n边形,除去一个内角后,其余的(n-1)个内角的和是1035°,则除去的这个内角的度数为 。这个多边形为 边形。
1035°÷180°=
华师大版七年级下册9.2 多边形的内角和与外角和说课ppt课件: 这是一份华师大版七年级下册<a href="/sx/tb_c14890_t3/?tag_id=26" target="_blank">9.2 多边形的内角和与外角和说课ppt课件</a>,共32页。PPT课件主要包含了n–2,从图中可以知道,n·180°等内容,欢迎下载使用。
初中数学苏科版七年级下册第7章 平面图形的认识(二)7.5 多边形的内角和与外角和图文课件ppt: 这是一份初中数学苏科版七年级下册<a href="/sx/tb_c88672_t3/?tag_id=26" target="_blank">第7章 平面图形的认识(二)7.5 多边形的内角和与外角和图文课件ppt</a>,共34页。PPT课件主要包含了知识点,三角形的内角和,真题1,多边形的内角和,真题2,真题3,多边形的外角和,真题4等内容,欢迎下载使用。
华师大版七年级下册9.2 多边形的内角和与外角和完整版课件ppt: 这是一份华师大版七年级下册<a href="/sx/tb_c14890_t3/?tag_id=26" target="_blank">9.2 多边形的内角和与外角和完整版课件ppt</a>,文件包含922多边形的内角和与外角和pptx、922多边形的内角和与外角和教学设计doc、922多边形的内角和与外角和学案doc等3份课件配套教学资源,其中PPT共23页, 欢迎下载使用。













