



- 【寒假作业】人教A版2019 高中数学 高二寒假提升训练专题03 函数的单调性(五大考点)-练习 试卷 4 次下载
- 【寒假作业】人教A版2019 高中数学 高二寒假提升训练专题04 函数的极值与最大(小)值 (十二大考点)-练习 试卷 4 次下载
- 【寒假作业】人教A版2019 高中数学 高二寒假提升训练专题06 分类加法计数原理与分步乘法计数原理(八大考点)-练习 试卷 3 次下载
- 【寒假作业】人教A版2019 高中数学 高二寒假提升训练专题07 排列组合(十五大考点)-练习 试卷 3 次下载
- 【寒假作业】人教A版2019 高中数学 高二寒假提升训练专题08 二项式定理(八大考点)-练习 试卷 3 次下载
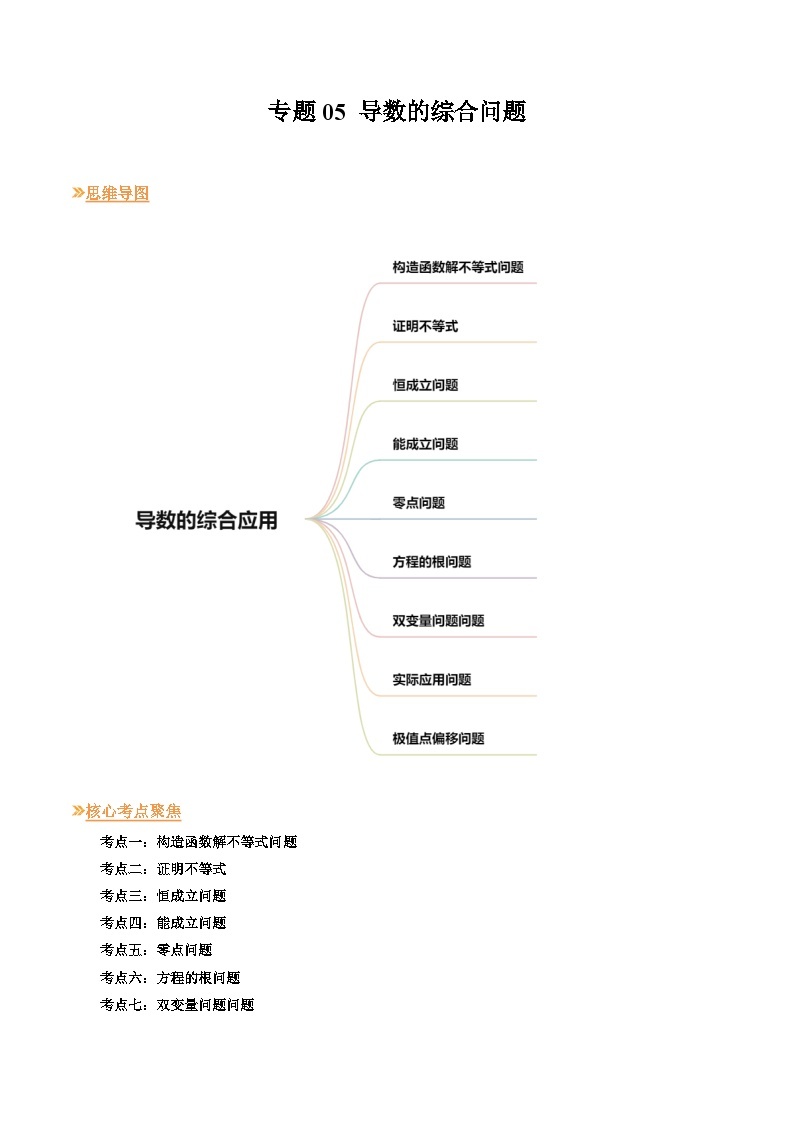
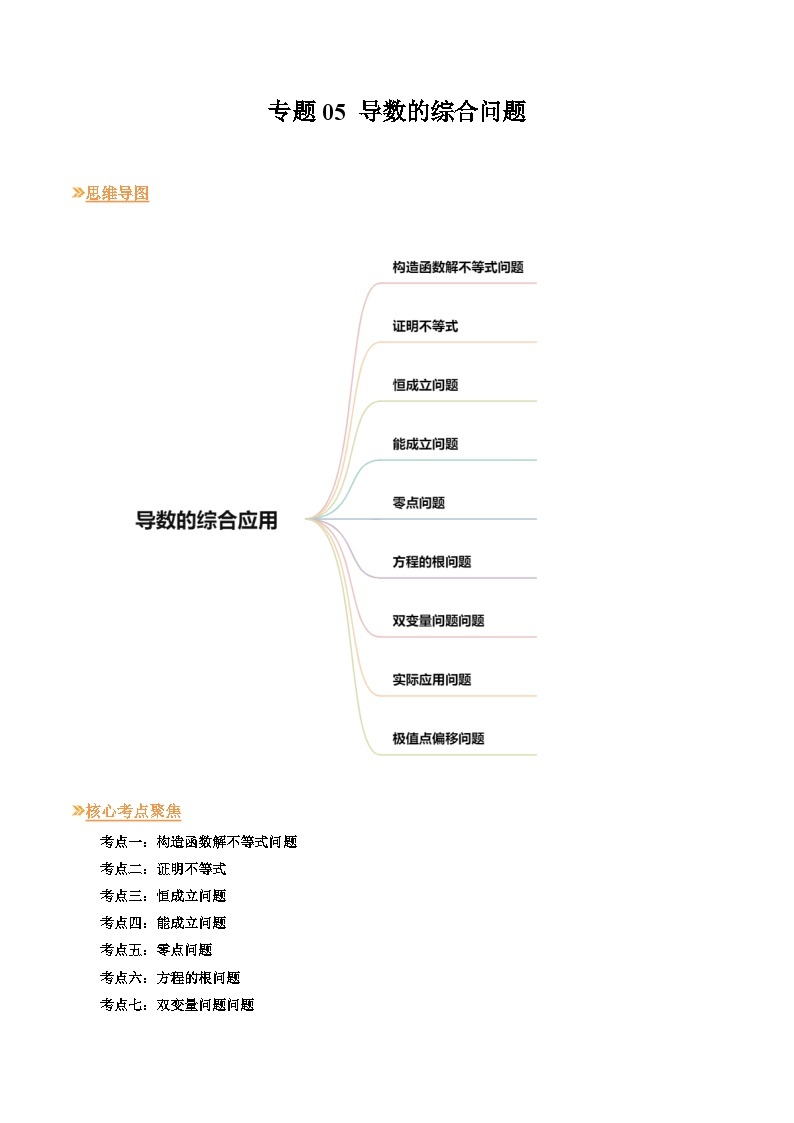
【寒假作业】人教A版2019 高中数学 高二寒假提升训练专题05 导数的综合问题(九大考点)-练习
展开思维导图
核心考点聚焦
考点一:构造函数解不等式问题
考点二:证明不等式
考点三:恒成立问题
考点四:能成立问题
考点五:零点问题
考点六:方程的根问题
考点七:双变量问题问题
考点八:实际应用问题
考点九:极值点偏移问题
1、恒成立问题
(1)若函数在区间D上存在最小值和最大值,则
不等式在区间D上恒成立;
不等式在区间D上恒成立;
不等式在区间D上恒成立;
不等式在区间D上恒成立;
(2)若函数在区间D上不存在最大(小)值,且值域为,则
不等式在区间D上恒成立.
不等式在区间D上恒成立.
(3)若函数在区间D上存在最小值和最大值,即,则对不等式有解问题有以下结论:
不等式在区间D上有解;
不等式在区间D上有解;
不等式在区间D上有解;
不等式在区间D上有解;
(4)若函数在区间D上不存在最大(小)值,如值域为,则对不等式有解问题有以下结论:
不等式在区间D上有解
不等式在区间D上有解
(5)对于任意的,总存在,使得;
(6)对于任意的,总存在,使得;
(7)若存在,对于任意的,使得;
(8)若存在,对于任意的,使得;
(9)对于任意的,使得;
(10)对于任意的,使得;
(11)若存在,总存在,使得
(12)若存在,总存在,使得.
2、破解双参数不等式的方法:
一是转化,即由已知条件入手,寻找双参数满足的关系式,并把含双参数的不等式转化为含单参数的不等式;
二是巧构函数,再借用导数,判断函数的单调性,从而求其最值;
三是回归双参的不等式的证明,把所求的最值应用到双参不等式,即可证得结果.
3、函数零点问题的常见考点:判断函数是否存在零点或者求零点的个数;根据含参函数零点情况,求参数的值或取值范围.
求解步骤:
第一步:将问题转化为函数的零点问题,进而转化为函数的图像与轴(或直线)在某区间上的交点问题;
第二步:利用导数研究该函数在此区间上的单调性、极值、端点值等性质,进而画出其图像;
第三步:结合图像判断零点或根据零点分析参数.
1、极值点偏移的相关概念
所谓极值点偏移,是指对于单极值函数,由于函数极值点左右的增减速度不同,使得函数图像没有对称性.若函数在处取得极值,且函数与直线交于两点,则的中点为,而往往.如下图所示.
图1 极值点不偏移 图2 极值点偏移
极值点偏移的定义:对于函数在区间内只有一个极值点,方程的解分别为,且,(1)若,则称函数在区间上极值点偏移;(2)若,则函数在区间上极值点左偏,简称极值点左偏;(3)若,则函数在区间上极值点右偏,简称极值点右偏.
2、利用导数证明不等式问题,方法如下:
(1)直接构造函数法:证明不等式(或)转化为证明(或),进而构造辅助函数;
(2)适当放缩构造法:一是根据已知条件适当放缩;二是利用常见放缩结论;
(3)构造“形似”函数,稍作变形再构造,对原不等式同解变形,根据相似结构构造辅助函数.
(4)对数单身狗,指数找基友
(5)凹凸反转,转化为最值问题
(6)同构变形
考点剖析
考点一:构造函数解不等式问题
例1.(2024·陕西西安·高二统考)已知是函数的导函数,,且对于任意的有.请你试用构造函数的方法,利用函数的单调性判断下列不等式一定成立的是( )
A.B.
C.D.
【答案】A
【解析】令,,则,
故在上单调递增,
而,故,故是偶函数,
故,
即,
故A正确,BCD错误,
故选:A.
例2.(2024·全国·高三专题练习)若函数在R上可导,且满足恒成立,常数则下列不等式一定成立的是( )
A.B.
C.D.
【答案】A
【解析】令,则恒成立,故在上单调递增.
,
,即.
故选:A
例3.(2024·湖北武汉·高二武汉市育才高级中学校联考期末)已知定义域为的奇函数的图象是一条连续不断的曲线,当时,,当时,,且,则关于的不等式的解集为( )
A.B.
C.D.
【答案】D
【解析】因为当时,,所以在单调递减;
当时,,所以在单调递增,
因为定义域为的奇函数,则过点,且,则过点,
由奇函数的图象关于原点对称,画出示意图如下:
或,
故选:D.
考点二:证明不等式
例4.(2024·浙江·高三专题练习)证明以下不等式:
(1);
(2);
(3).
【解析】(1)令,则有.
令,即,解得;
令,即,解得,
所以在单调递减,上单调递增,
所以,即.
所以.
(2)令,则.
令,即,解得;
令,即,解得,
所以在单调递增,上单调递减,
所以,即,
所以.
(3)由(1)得,所以(当且仅当时取等号)①.
由(2)得,所以(当且仅当时取等号)②
因为①式与②式取等号的条件不同,所以.
例5.(2024·全国·高二专题练习)当时,证明:不等式.
【解析】设,其中,则,
故函数在上为增函数,所以,,
故对任意的,.
例6.(2024·山东菏泽·高二校考阶段练习)已知函数在处取得极值.
(1)求实数的值;
(2)证明:对于任意的正整数,不等式成立.
【解析】(1),
为的极值点,
.
当时,,
,
令,当,
的增区间是,减区间是,
符合题意.
(2)由(1)知当时,,即,
令,则,即,
,
即.
考点三:恒成立问题
例7.(2024·天津·高二天津市西青区杨柳青第一中学校联考期末)已知函数其中为常数.
(1)当时,求曲线在点处的切线方程;
(2)求的单调区间;
(3)若对任意,不等式恒成立,求的取值范围.
【解析】(1)当时,,则
,,
所以,
所以曲线在点处的切线方程为,
(2)的定义域为,
由,得,
当时,,当时,,
所以的递增区间为,递减区间为,
(3)由(2)可知当取得最大值,
因为对任意,不等式恒成立,
所以,即,,
解得或,
即的取值范围为.
例8.(2024·全国·高三专题练习)已知函数,其图象在点处的切线方程为.
(1)求,的值与函数的单调区间;
(2)若对,,不等式恒成立,求的取值范围.
【解析】(1),
,
函数的图象在点处的切线方程为.
解得,.
,
令,解得或;令,解得.
函数的单调递增区间为,;单调递减区间为.
(2)由(1)可得:,.
令,则,
所以当变化时,的变化情况如下:
由表格可知:当时,函数取得极大值,,又.
函数在上的最大值为8.
由,不等式恒成立,.
,
解得或.
的取值范围是.
例9.(2024·陕西榆林·高二校考)已知函数,.
(1)当时,求函数的极值;
(2)若对任意,不等式恒成立,求的取值范围.
【解析】(1)当时,,则,
令,得,令,得
∴函数在上单调递增,在上单调递减,
∴函数的极大值为,无极小值;
(2)
当,,则是增函数.
当时,则是减函数,
∴的最大值为,
∵恒成立,
∴,解得,
∴的取值范围为.
考点四:能成立问题
例10.(2024·四川雅安·高二雅安中学校考阶段练习)已知函数.
(1)若,求函数的极小值.
(2)存在,使得成立,求实数的取值范围.
【解析】(1)当时,则,令,得.
时,函数的单调递增区间为,
时,函数的单调递减区间为;
所以函数的极小值为.
(2)由题设,在上,
设,则,显然当时恒成立,
所以在单调递增,则,
综上,,故.
例11.(2024·重庆铜梁·高二铜梁一中校考阶段练习)已知函数在处取得极值,其中为常数.
(1)试确定的值;
(2)讨论函数的单调区间;
(3)若对任意,不等式有解,求的取值范围.
【解析】(1)由题意知,因此,从而.
由题意求导得,因此,解得;
(2)由(1)知.令,解得.
因此的单调递增区间为,而的单调递减区间为;
(3)由(2)知,在处取得极大值,此极大值也是最最值.
要使()有解,只需.
即,从而.
解得.
所以的取值范围为.
例12.(2024·陕西西安·高三阶段练习)已知函数.
(1)若,求曲线在处切线的方程;
(2)求的单调区间;
(3)设,若对任意,均存在,使得,求的取值范围.
【解析】(1)由已知,
,
曲线在处切线方程为,即.
(2).
①当时,由于,故,
所以,的单调递增区间为,无单调递减区间.
②当时,由,得.
在区间上,,在区间上,
所以,函数的单调递增区间为,单调递减区间为.
(3)由已知,转化为,
由(2)知,当时,在上单调递增,值域为,故不符合题意.
(或者举出反例:存在,故不符合题意.)
当时,在上单调递增,在上单调递减,
故的极大值即为最大值,,
所以,
解得.
考点五:零点问题
例13.(2024·四川·高三统考对口高考)已知a,b为实数,是定义在R上的奇函数.
(1)求a,b的值;
(2)证明:函数有唯一零点.
【解析】(1)因函数是定义在R上的奇函数,则,,
因此,恒成立,所以.
(2)由(1)知,,,在上单调递增,则函数至多有一个零点,
又,所以函数有唯一零点.
例14.(2024·四川资阳·高二校考)已知三次函数的极大值是,其导函数的图象经过点,如图所示,求
(1),,的值;
(2)若函数有三个零点,求的取值范围.
【解析】(1)由导函数的图象可知:
当时,,函数单调递增;
当时,,函数单调递减;
当时,,函数单调递增,
所以是函数的极大值点,是函数的极小值点,
于是有,
由,
所以有;
(2)由(1)函数的极小值为,极大值为,
而知函数的图象如下图所示
因为函数有三个零点,
所以函数的图象与直线有三个不同的交点,
所以.
例15.(2024·青海西宁·统考二模)已知函数.
(1)讨论的单调性;
(2)若恰有一个零点,求a的值.
【解析】(1),
令,得.
因为,则,即原方程有两根设为
,所以(舍去),.
则当时,,当时,
在上是减函数,在上是增函数.
(2)由(1)可知.
①若,则,即,可得,
设,在上单调递减
所以至多有一解且,则,
代入解得.
②若,则,即,可得,
结合①可得,
因为,,
所以在存在一个零点.
当时,,
所以在存在一个零点.因此存在两个零点,不合题意
综上所述:.
考点六:方程的根问题
例16.(2024·四川乐山·高二期末)已知函数.
(1)求的极值;
(2)求方程有两个不同的根,求的取值范围.
【解析】(1)∵,
∴的定义域为,,
令,解得.
则当时,单调递减,当时,单调递增,
∴在单调递减,在单调递增.
∴当时,有极小值,没有极大值.
(2)∵时,,时,,
则的图象如下:
由图象可知,当时,方程有两个不同的根.
故的取值范围为.
例17.(2024·北京大兴·高二统考)已知函数.
(1)求的极值;
(2)比较的大小,并画出的大致图像;
(3)若关于的方程有实数解,直接写出实数的取值范围.
【解析】(1)的定义域为,,
于是时,单调递增;
时,单调递减,
又,则在处取到极小值,无极大值.
(2)由(1)知,在区间上单调递减.故.
又因为当时,,故,所以.
因为,所以.结合(1)中的单调性,大致图像如下:
(3)的解的个数可以看成和直线在同一坐标系下图像交点的个数,
由(2)的图像知,当的取值不小于最小值即可,即
例18.(2024·北京·高二北京市第三十五中学校考)已知函数.
(1)求的单调区间;
(2)求在区间上的最大值和最小值.
(3)若方程有三个根,写出k的取值范围(无需解答过程).
【解析】(1),
令可得或,
令可得,
故函数的增区间为和,减区间为.
(2)由(1)知,上递增,在递减,
故当时,,
又,故.
(3)由(1)(2)知函数在上递增,在上递减,在上递增,且极大值为,极小值为,
若方程有三个根,即与图象有3个交点,
故k的取值范围为.
考点七:双变量问题问题
例19.(2024·四川凉山·高二宁南中学校联考期末)已知函数.
(1)讨论函数的单调性;
(2)若恒成立,求的取值范围.
【解析】(1)由,
若,则恒成立,即在上单调递增,
若,令得,即在上单调递增,
令得,即在上单调递减,
综上所述当时,在上单调递增;
当时,在上单调递增,在上单调递减;
(2)由(1)得当时,在上单调递增,
当趋近于时,趋近于,不符合题意,
故,则,
所以,
令,
显然当时,,时,,故在时单调递减,
在上单调递增,即,
所以,即
例20.(2024·黑龙江哈尔滨·高二哈九中校考阶段练习)已知,函数.
(1)当与都存在极小值,且极小值之和为0时,求实数的值;
(2)当时,若,求证:
【解析】(1),定义域均为,
,
当时,则,在单调递增,无极值,与题不符;
当时,令,解得:,
所以在单调递减,在单调递增,
在取极小值,且;
又,
当时:,在单调递减,无极值,与题不符;
当时:令,解得:,
所以在单调递减,在单调递增,
在取极小值,且;
依题意,
解得:,
(2)当时,,
由题意可知,,两式相减得,
整理为,
要证明,即证明,
不妨设,即证明,即,
设,即证明,
设,
,
所以函数在区间单调递减,且,
即在区间恒成立,即,
即,得证.
例21.(2024·吉林长春·高二长春市第五中学校考阶段练习)已知函数.
(1)求函数的单调区间;
(2)对任意的、,当时都有,求实数的取值范围.
【解析】(1)函数定义域为,.
当时,对任意的,,所以,函数的减区间为,无增区间;
当时,由得,由得.
此时函数的增区间为,减区间为.
综上所述,当时,函数的减区间为,无增区间;
当时,函数的增区间为,减区间为.
(2)由,即.
令,
因为,则,所以,函数在上单调递增,
所以,在上恒成立,即在上恒成立,
只需,
设,,在单调递增,所以.
综上所述,实数的取值范围为.
考点八:实际应用问题
例22.(2024·江苏盐城·高二江苏省射阳中学校考阶段练习)已知某商品的成本和产量满足关系(元),该商品的销售单价和产量满足关系式(元),记该商品的利润为(假设生产的商品能全部售出,利润=销售额-成本).
(1)将利润(元)表示为产量的函数;
(2)当产量为多少时,可获得最大利润?最大利润是多少万元?
【解析】(1)由题意可知,
,
(2)因为,由,解得.
当时,单调递增;
当时,单调递减.
所以当时,取得最大值,且最大值为315万元.
答:当产量为200时,可获得最大利润为315万元.
例23.(2024·全国·高二专题练习)为进一步推进国家森林城市建设,我市准备制定生态环境改造投资方案,该方案要求同时具备下列两个条件:①每年用于风景区改造的费用随每年改造生态环境总费用增加而增加;②每年用于风景区改造的费用不得低于每年改造生态环境总费用的,但不得高于每年改造生态环境总费用的.若每年改造生态环境的总费用至少亿元,至多亿元;请你分析能否采用函数模型作为生态环境改造投资方案.
【解析】因为,,
所以当时,函数是增函数,满足条件①.
设,
则
令,得.
当变化时,,的变化情况,如下表:
当时,有最小值为,
当时,,
当时,,满足条件②.
所以能采用函数模型作为生态环境改造投资方案.
考点九:极值点偏移问题
例24.(2024·河北唐山·高三开滦第二中学校考阶段练习)已知函数.
(1)若函数有两个零点,求的取值范围;
(2)设是函数的两个极值点,证明:.
【解析】(1),
该方程有两个不等实根,由,
所以直线与函数的图象有两个不同交点,
由,
当时,单调递减,
当时,单调递增,因此,
当时,,当,,
如下图所示:
所以要想有两个不同交点,只需,即的取值范围为;
(2)因为是函数的两个极值点,
所以,由(1)可知:,不妨设,
要证明,只需证明,显然,
由(2)可知:当时,单调递增,所以只需证明,
而,所以证明即可,
即证明函数在时恒成立,
由,
显然当时,,因此函数单调递减,
所以当时,有,所以当时,恒成立,因此命题得以证明.
例25.(2024·四川南充·高二统考期末)设函数.
(1)当时,讨论函数的单调性;
(2)设,记,当时,若方程有两个不相等的实根,求证:.
【解析】(1)的定义域为,
.
令,则得到导函数的两个零点,或,由于分母为正,
故我们只关注分子函数,其为二次函数,借助其图像,
以两个零点的大小关系为分类标准得到如下:
①当时,即时,当时,,单调递减,
当时,,单调递增;
②当时,即时,恒成立,即恒成立,故在上单调递增;
综上所述,当时,的单减区间为,单增区间为;
当时,只有单增区间;
(2)由题可知,,
设是方程的两个不等实根,不妨设为,
则,两式相减整理得到
,从而得到,
要证,故只需要证明,
由于,
转化为,
即,即,
令,则上述式子转化为
设,则,
当且仅当时等号成立,故在上单调递增,故有,
故得证,
即.
例26.(2024·广东深圳·高三校联考阶段练习)已知函数
(1)若对任意的,都有恒成立,求实数的取值范围;
(2)设是两个不相等的实数,且.求证:
【解析】(1)当时,,
因为,所以,即,不符合题意;
当时,,
当时,,当时,,
所以在上单调递增,在上单调递减.
所以.
由恒成立可知,所以.
又因为,所以的取值范围为.
(2)因为,所以,即.
令,由题意可知,存在不相等的两个实数,,使得.
由(1)可知在区间上单调递增,在区间上单调递减.
不妨设,则.
设,
则,
所以在上单调递增,
所以,即在区间上恒成立.
因为,所以.
因为,所以.
又因为,,且在区间上单调递增,
所以,即.
过关检测
1.(2024·陕西西安·高二校考)已知函数的定义域为,其导函数是.若恒成立,则关于的不等式的解集为( )
A.B.
C.D.
【答案】A
【解析】令,
则,
所以函数在定义域内为单调递增,
因为,所以关于的不等式
可转化为,即,
因为,所以,
即不等式的解集为.
故选:A
2.(2024·湖北·高二校联考)已知函数的定义域为,其导函数是.有,则关于x的不等式的解集为( )
A.B.C.D.
【答案】B
【解析】令,
,
因为,
所以,
所以在上单调递减,
又,
所以,
解得
所以.
故选:B
3.(2024·陕西商洛·高二校考)已知函数.
(1)当时,求函数的最小值;
(2)当时,证明:不等式在上恒成立.
【解析】(1)当时,,则,令,得,
当时,,单调递减,当时,,单调递增,
故当时,取得最小值为.
(2),且,,
设,,,,
故在上恒成立,故单调递增,,
故在上单调递增,恒成立.
4.(2024·江西南昌·高三校联考阶段练习)已知函数.
(1)讨论函数的单调性;
(2)当时,证明:不等式.
【解析】(1)定义域为,,
①若恒成立,即恒成立,因为,所以恒成立,所以,因为,当且仅当即时,等号成立,所以,即时,在上是单调递增;
②当时,则的根为,,
由,得,,由,得或,,得.∴在,上单调递增,在上单调递减.
综上,时,在上是单调递增;
时,在,上单调递增;在上单调递减.
(2)要证,只须证.
∵,即证.
法一:∵,∴只需证,
则,令,恒成立,
∴在上单调递增,又,.
∴使,即,∴.
当时,,即;当时,,即,
∴在上单调递减,在上单调递增,
∴.
∴,得证.
法二:令,只须证.
,令,则.∵,∴,∴在上单调递增.
又∵,而,∴,使,∴,即.
∵,在上单调递增,∴,即,
又知,知.当时,;当时,,∴在上单调递减,在上单调递增,∴,得证.
5.(2024·安徽芜湖·高二安徽师范大学附属中学校考)已知函数在与处都取得极值.
(1)求,的值;
(2)若对任意,不等式恒成立,求实数的取值范围.
【解析】(1)由题设,,又,,解得,.
(2)由,知,即,
当时,,随的变化情况如下表:
∴在上单调递增,在上单调递减,在上单调递增,
∴当时,为极大值,又,则为在上的最大值,
要使对任意恒成立,则只需,解得或,
∴实数的取值范围为.
6.(2024·重庆沙坪坝·高二重庆八中校考阶段练习)已知函数.
(1)求函数在区间上的最大值和最小值(参考数据:);
(2)若不等式有解,求实数a的取值范围.
【解析】(1)求导得:,令可得,令可得
,于是函数在单调递增,在单调递减,
于是当时,取最大值为,
又,,于是当时,取最小值为
综上:当时,取最大值为,当时,取最小值为
(2)原不等式即为:,可化简为
记,则原不等式有解可转化为的最大值
求导得:,于是函数在上单调递增,在上单调递减
于是:,于是,解得:.
7.(2024·重庆沙坪坝·高二重庆南开中学校考)已知函数,.
(1)求函数的单调区间;
(2)若函数在上有两个不同的零点,求实数的取值范围.
【解析】(1)因为,所以,
所以当或时,当时,
所以的单调递增区间为和,单调递减区间为.
(2)由(1)可知在上单调递减,在上单调递增,
所以,又,,
因为函数在上有两个不同的零点,
所以,即,解得,即实数的取值范围为.
8.(2024·浙江杭州·高二浙江省杭州第二中学校联考)已知函数.
(1)求曲线在处的切线方程;
(2)方程恰有两个不同的实根,求的取值范围.
【解析】(1)依题意,,
,
所以,又,所以切线方程为.
(2)因为,
所以:
当时,,所以单调递增;
当时,,所以单调递减.
所以在处取得极大值也即是最大值,
对于函数,
,,当时,;当时,.
所以的取值范围是.
9.(2024·广东揭阳·高二惠来县第一中学校考阶段练习)设函数.
(1)当时,求函数的单调区间;
(2)若函数有两个极值点,且,求的最小值.
【解析】(1)当时,,则定义域为,,
当时,;当时,;
的单调递增区间为,;单调递减区间为.
(2)定义域为,,
有两个极值点等价于在上有两个不等实根,
,,,,
;
设,
则,
在上单调递减,,
即,
的最小值为.
10.(2024·高二单元测试)某企业拟建造如图所示的容器(不计厚度,长度单位:m),其中容器的中间为圆柱体,左右两端均为半球体,按照设计要求容器的体积为m3.假设该容器的建造费用仅与其表面积有关.已知圆柱体部分每平方米建造费用为3万元,半球体部分每平方米建造费用为4万元.设该容器的总建造费用为y万元.
(1)将y表示成r的函数,并求该函数的定义域;
(2)确定r和l为何值时,该容器的建造费用最小,并求出最小建造费用.
【解析】(1)由题意可知,,∴,
又圆柱的侧面积为,两端两个半球的表面积之和为,
所以,
又,,
所以定义域为.
(2)因为,
所以令,得,令,得,
又定义域为,所以函数在上单调递减,在上单调递增,
所以当米时,该容器的建造费用最小,为万元,此时m.
11.(2024·黑龙江牡丹江·高二牡丹江市第二高级中学校考阶段练习)某汽车公司生产一种品牌汽车,上年度成本价为10万元/辆,出厂价为13万元/辆,年销售量为5万辆.本年度公司为了进一步扩大市场占有量,计划降低成本,实行降价销售.设本年度成本价比上年度降低了,本年度出厂价比上年度降低了.
(1)若本年度年销售量比上年度增加了倍,问在什么取值范围时,本年度的年利润比上年度有所增加?
(2)若本年度年销售量关于的函数为,则当为何值时,本年度年利润最大?
【解析】(1)本年度年利润为.
要使本年度的年利润比上年度有所增加,则有.
解得.
(2)本年度年利润为
.
令,解得.又.
所以函数在上为增函数,在上为减函数.
故当时,取得最大值,即当时,本年度的年利润最大.
12.(2024·河南平顶山·汝州市第一高级中学校考模拟预测)已知函数有两个零点.
(1)求a的取值范围;
(2)设是的两个零点,证明:.
【解析】(1)由,得,
设,则,,
因为,所以当时,,当时,,
所以在上单调递减,在上单调递增.
又因为,所以,
,
,
所以a的取值范围是.
(2)证明:不妨设,
由(1)知,则,,,
又在上单调递增,
所以等价于,即.
设,
则.
设,则,
设,则,当时,,单调递减,
当时,,单调递增,又因为,,,
所以存在,使得,当时,,即,
当时,,即,
所以在上单调递减,在上单调递增.
又因为,,
所以当时,,当时,,
所以当时,,单调递减,
因为,所以,
所以,即原命题得证.
13.(2024·辽宁丹东·统考模拟预测)已知函数.
(1)若,证明:;
(2)若有两个不同的零点,求a的取值范围,并证明:.
【解析】(1)当时,,定义域为
令,则
当时,;当时,;
所以函数在上单调递增,在上单调递减,
故,所以,得;
(2)因为有两个不同的零点,则在定义域内不单调;
由
当时,在恒成立,则在上单调递减,不符合题意;
当时,在上有,在上有,
所以在上单调递增,在上单调递减.不妨设
令
则
当时,,则在上单调递增
所以
故,因为
所以,又,
则,又在上单调递减,
所以,则.
,
0
2
,
0
0
单调递增
极大值
单调递减
极小值
单调递增
1
+
0
-
极大值
1
+
0
-
0
+
递增
极大值
递减
极小值
递增
【寒假作业】人教A版2019 高中数学 高二寒假提升训练专题09 条件概率与全概率公式(五大考点)-练习: 这是一份【寒假作业】人教A版2019 高中数学 高二寒假提升训练专题09 条件概率与全概率公式(五大考点)-练习,文件包含寒假作业人教A版2019高中数学高二寒假提升训练专题09条件概率与全概率公式五大考点原卷版docx、寒假作业人教A版2019高中数学高二寒假提升训练专题09条件概率与全概率公式五大考点解析版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。
【寒假作业】人教A版2019 高中数学 高二寒假提升训练专题08 二项式定理(八大考点)-练习: 这是一份【寒假作业】人教A版2019 高中数学 高二寒假提升训练专题08 二项式定理(八大考点)-练习,文件包含寒假作业人教A版2019高中数学高二寒假提升训练专题08二项式定理八大考点原卷版docx、寒假作业人教A版2019高中数学高二寒假提升训练专题08二项式定理八大考点解析版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
【寒假作业】人教A版2019 高中数学 高二寒假提升训练专题07 排列组合(十五大考点)-练习: 这是一份【寒假作业】人教A版2019 高中数学 高二寒假提升训练专题07 排列组合(十五大考点)-练习,文件包含寒假作业人教A版2019高中数学高二寒假提升训练专题07排列组合十五大考点原卷版docx、寒假作业人教A版2019高中数学高二寒假提升训练专题07排列组合十五大考点解析版docx等2份试卷配套教学资源,其中试卷共48页, 欢迎下载使用。