


题型06 最值问题之瓜豆原理-2023年中考数学重难点专题最后冲刺之最值问题(全国通用)
展开06最值问题之瓜豆原理
知识解读
瓜豆原理是主从动点联动问题,也叫旋转相似,这类问题在解答的时候需要有轨迹思想,就是先要明确主动点的轨迹,然后要搞清楚主动点和从动点的关系,进而确定从动点的轨迹来解决问题.
瓜豆原理:一个主动点,一个从动点(根据某种约束条件,跟着主动点动),当主动点运动时,从动点的轨迹相同.(古人云:种瓜得瓜,种豆得豆.“种”圆得圆,“种”线得线,谓之“瓜豆原理”.)
满足条件:
1.两动一定;2.动点与定点的连线夹角是定角;3.动点到定点的距离比值是定值.
方法:
第一步:找主动点的轨迹 ;
第二步:找从动点与主动点的关系;
第三步:找主动点的起点和终点;第四步:通过相似确定从动点的轨迹;
第五步:根据轨迹确定点线、点圆最值.
“瓜豆原理”其实质就是构造旋转、相似.
涉及的知识和方法:
知识:①相似;②三角形的两边之和大于第三边;③点到直线之间的距离垂线段最短;④点到圆上点共线有最值.
模型一:运动轨迹为圆弧
引例1:如图,P是圆O上一个动点,A为定点,连接AP,Q为AP中点.
考虑:当点P在圆O上运动时,Q点轨迹是?
【分析】观察动图可知点Q轨迹是个圆,而我们还需确定的是此圆与圆O有什么关系?
考虑到Q点始终为AP中点,连接AO,取AO中点M,则M点即为Q点轨迹圆圆心,半径MQ是OP一半,任意时刻,均有△AMQ∽△AOP,QM:PO=AQ:AP=1:2.
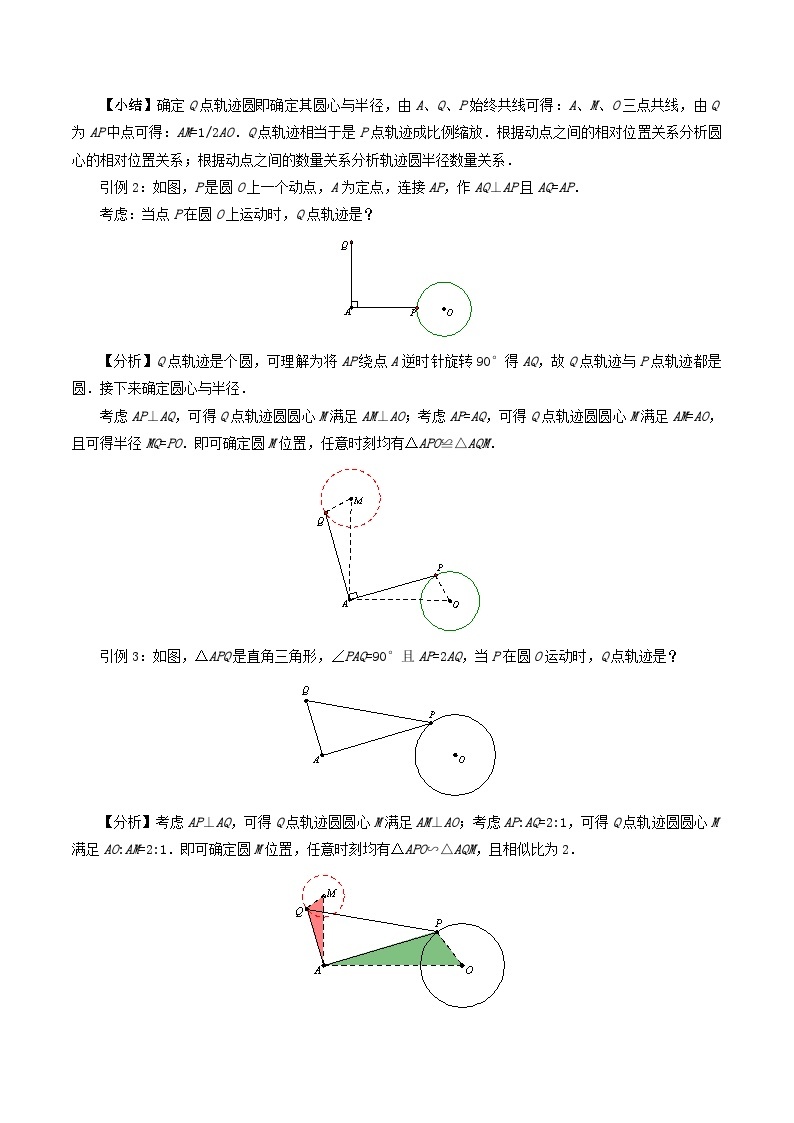
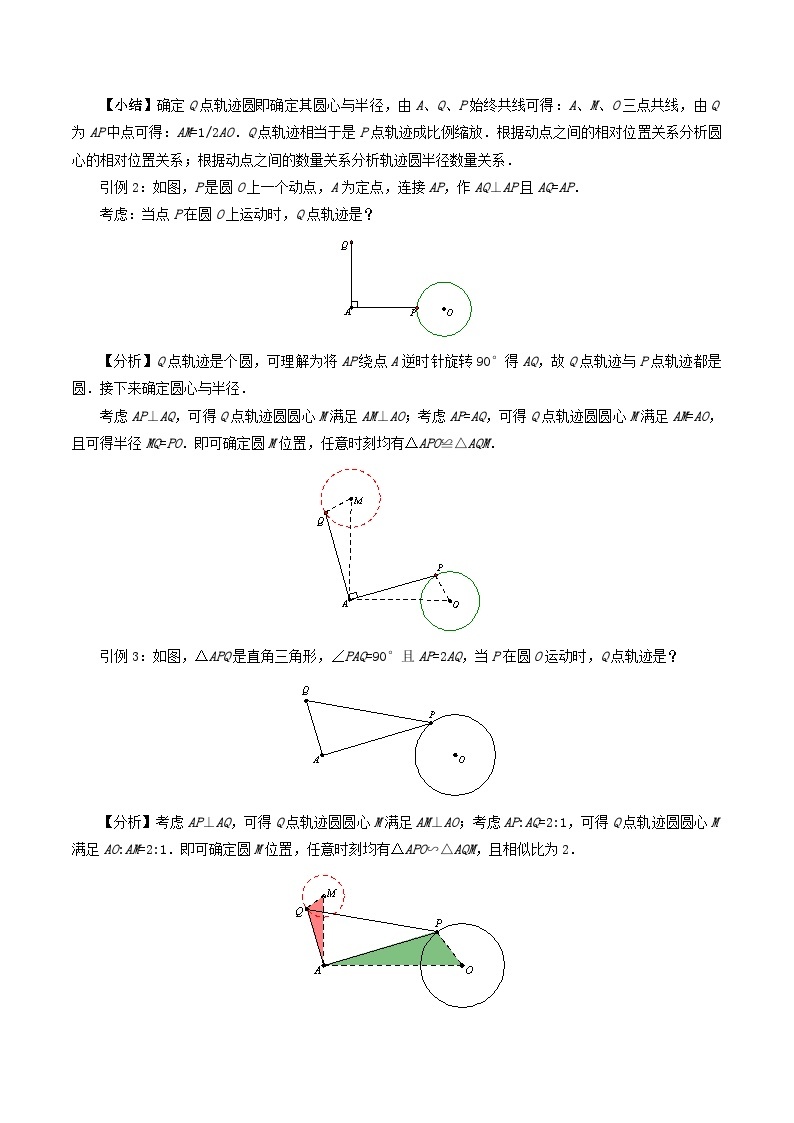
【小结】确定Q点轨迹圆即确定其圆心与半径,由A、Q、P始终共线可得:A、M、O三点共线,由Q为AP中点可得:AM=1/2AO.Q点轨迹相当于是P点轨迹成比例缩放.根据动点之间的相对位置关系分析圆心的相对位置关系;根据动点之间的数量关系分析轨迹圆半径数量关系.
引例2:如图,P是圆O上一个动点,A为定点,连接AP,作AQ⊥AP且AQ=AP.
考虑:当点P在圆O上运动时,Q点轨迹是?
【分析】Q点轨迹是个圆,可理解为将AP绕点A逆时针旋转90°得AQ,故Q点轨迹与P点轨迹都是圆.接下来确定圆心与半径.
考虑AP⊥AQ,可得Q点轨迹圆圆心M满足AM⊥AO;考虑AP=AQ,可得Q点轨迹圆圆心M满足AM=AO,且可得半径MQ=PO.即可确定圆M位置,任意时刻均有△APO≌△AQM.
引例3:如图,△APQ是直角三角形,∠PAQ=90°且AP=2AQ,当P在圆O运动时,Q点轨迹是?
【分析】考虑AP⊥AQ,可得Q点轨迹圆圆心M满足AM⊥AO;考虑AP:AQ=2:1,可得Q点轨迹圆圆心M满足AO:AM=2:1.即可确定圆M位置,任意时刻均有△APO∽△AQM,且相似比为2.
【模型总结】
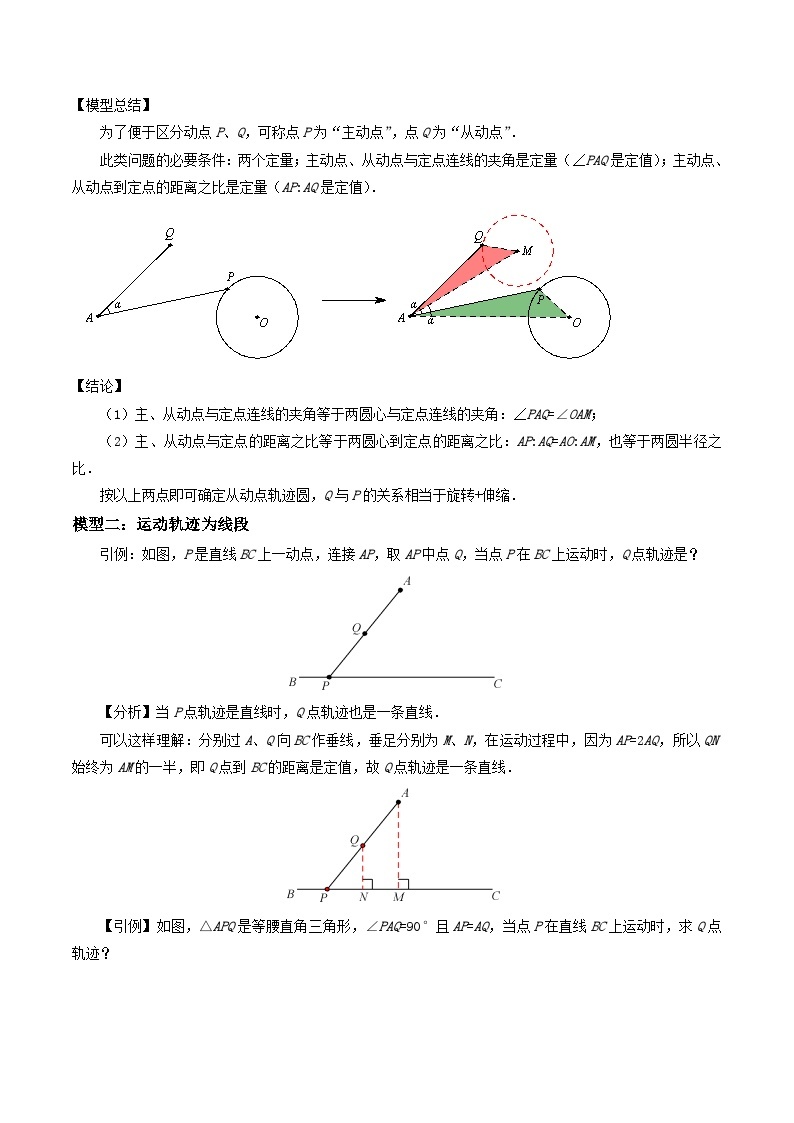
为了便于区分动点P、Q,可称点P为“主动点”,点Q为“从动点”.
此类问题的必要条件:两个定量;主动点、从动点与定点连线的夹角是定量(∠PAQ是定值);主动点、从动点到定点的距离之比是定量(AP:AQ是定值).
【结论】
(1)主、从动点与定点连线的夹角等于两圆心与定点连线的夹角:∠PAQ=∠OAM;
(2)主、从动点与定点的距离之比等于两圆心到定点的距离之比:AP:AQ=AO:AM,也等于两圆半径之比.
按以上两点即可确定从动点轨迹圆,Q与P的关系相当于旋转+伸缩.
模型二:运动轨迹为线段
引例:如图,P是直线BC上一动点,连接AP,取AP中点Q,当点P在BC上运动时,Q点轨迹是?
【分析】当P点轨迹是直线时,Q点轨迹也是一条直线.
可以这样理解:分别过A、Q向BC作垂线,垂足分别为M、N,在运动过程中,因为AP=2AQ,所以QN始终为AM的一半,即Q点到BC的距离是定值,故Q点轨迹是一条直线.
【引例】如图,△APQ是等腰直角三角形,∠PAQ=90°且AP=AQ,当点P在直线BC上运动时,求Q点轨迹?
【分析】当AP与AQ夹角固定且AP:AQ为定值的话,P、Q轨迹是同一种图形.
当确定轨迹是线段的时候,可以任取两个时刻的Q点的位置,连线即可,比如Q点的起始位置和终点位置,连接即得Q点轨迹线段.
【模型总结】
必要条件:
主动点、从动点与定点连线的夹角是定量(∠PAQ是定值);
主动点、从动点到定点的距离之比是定量(AP:AQ是定值).
结论:
P、Q两点轨迹所在直线的夹角等于∠PAQ(当∠PAQ≤90°时,∠PAQ等于MN与BC夹角)
P、Q两点轨迹长度之比等于AP:AQ(由△ABC∽△AMN,可得AP:AQ=BC:MN)
针对训练
一、单选题
1.如图,A是上任意一点,点C在外,已知是等边三角形,则的面积的最大值为( )
A. B.4 C. D.6
【答案】A
【详解】解:如图,以为边向上作等边三角形,连接,
∵,
∴,即,
在和中,
,
∴,
∴,
∴点D的运动轨迹是以点M为圆心,长为半径的圆,要使的面积最大,则求出点D到线段的最大距离,
∵是边长为4的等边三角形,
∴点M到的距离为,
∴点D到的最大距离为,
∴的面积最大值是,
故选A.
2.如图,在矩形纸片ABCD中,,,点E是AB的中点,点F是AD边上的一个动点,将沿EF所在直线翻折,得到,则的长的最小值是
A. B.3 C. D.
【答案】D
【详解】以点E为圆心,AE长度为半径作圆,连接CE,当点在线段CE上时,的长取最小值,如图所示,
根据折叠可知:.
在中,,,,
,
的最小值.
故选D.
3.如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,BC=2 ,△ADC与△ABC关于AC对称,点E、F分别是边DC、BC上的任意一点,且DE=CF,BE、DF相交于点P,则CP的最小值为( )
A.1 B. C. D.2
【答案】D
【详解】解:连接AD,因为∠ACB=30°,所以∠BCD=60°,
因为CB=CD,所以△CBD是等边三角形,
所以BD=DC
因为DE=CF,∠EDB=∠FCD=60°,
所以△EDB≌△FCD,所以∠EBD=∠FDC,
因为∠FDC+∠BDF=60°,
所以∠EBD+∠BDF=60°,所以∠BPD=120°,
所以点P在以A为圆心,AD为半径的弧BD上,
直角△ABC中,∠ACB=30°,BC=2,所以AB=2,AC=4,
所以AP=2
当点A,P,C在一条直线上时,CP有最小值,
CP的最小值是AC-AP=4-2=2
故选D.
4.如图,等腰Rt△ABC中,斜边AB的长为2,O为AB的中点,P为AC边上的动点,OQ⊥OP交BC于点Q,M为PQ的中点,当点P从点A运动到点C时,点M所经过的路线长为( )
A. B. C.1 D.2
【答案】C
【详解】连接OC,作PE⊥AB于E,MH⊥AB于H,QF⊥AB于F,如图,
∵△ACB为等腰直角三角形,
∴AC=BC=AB=,∠A=∠B=45°,
∵O为AB的中点,
∴OC⊥AB,OC平分∠ACB,OC=OA=OB=1,
∴∠OCB=45°,
∵∠POQ=90°,∠COA=90°,
∴∠AOP=∠COQ,
在Rt△AOP和△COQ中
,
∴Rt△AOP≌△COQ,
∴AP=CQ,
易得△APE和△BFQ都为等腰直角三角形,
∴PE=AP=CQ,QF=BQ,
∴PE+QF=(CQ+BQ)=BC==1,
∵M点为PQ的中点,
∴MH为梯形PEFQ的中位线,
∴MH=(PE+QF)=,
即点M到AB的距离为,而CO=1,
∴点M的运动路线为△ABC的中位线,
∴当点P从点A运动到点C时,点M所经过的路线长=AB=1,
故选C.
5.如图,在平面直角坐标系中,Q是直线y=﹣x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点,连接,则的最小值为( )
A. B. C. D.
【答案】B
【详解】解:作QM⊥x轴于点M,Q′N⊥x轴于N,
设Q(,),则PM=,QM=,
∵∠PMQ=∠PNQ′=∠QPQ′=90°,
∴∠QPM+∠NPQ′=∠PQ′N+∠NPQ′,
∴∠QPM=∠PQ′N,
在△PQM和△Q′PN中,
,
∴△PQM≌△Q′PN(AAS),
∴PN=QM=,Q′N=PM=,
∴ON=1+PN=,
∴Q′(,),
∴OQ′2=()2+()2=m2﹣5m+10=(m﹣2)2+5,
当m=2时,OQ′2有最小值为5,
∴OQ′的最小值为,
故选:B.
二、填空题
6.如图,等边三角形ABC中,AB=4,高线AH=2,D是线段AH上一动点,以BD为边向下作等边三角形BDE,当点D从点A运动到点H的过程中,点E所经过的路径为线段CM,则线段CM的长为_______,当点D运动到点H,此时线段BE的长为__________.
【答案】
【详解】解:如图,连接EC.
∵△ABC,△BDE都是等边三角形,
∴BA=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABD=∠CBE,
在△ABD和△CBE中,
,
∴△ABD≌△CBE(SAS),
∴AD=EC,
∵点D从点A运动到点H,
∴点E的运动路径的长为,
当重合,而(即)为等边三角形,
故答案为:.
7.如图,在平面内,线段AB=6,P为线段AB上的动点,三角形纸片CDE的边CD所在的直线与线段AB垂直相交于点P,且满足PC=PA.若点P沿AB方向从点A运动到点B,则点E运动的路径长为________.
【答案】.
【详解】解:如图,由题意可知点C运动的路径为线段AC′,点E运动的路径为EE′,由平移的性质可知AC′=EE′,在Rt△ABC′中,易知AB=BC′=6,∠ABC′=90°,∴EE′=AC′==,故答案为.
8.如图,正方形的边长为4,为上一点,且,为边上的一个动点,连接,以为边向右侧作等边,连接,则的最小值为_______.
【答案】
【详解】由题意可知,点是主动点,点是从动点,点在线段上运动,点也一定在直线轨迹上运动
将绕点旋转,使与重合,得到,
从而可知为等边三角形,点在垂直于的直线上,
作,则即为的最小值,
作,可知四边形为矩形,
则.
故答案为.
9.如图,在Rt△ABC中,,,BC=2,线段BC绕点B旋转到BD,连AD,E为AD的中点,连接CE,则CE的最大值是________.
【答案】3
【详解】解:∵BC=2,线段BC绕点B旋转到BD,
∴BD=2,
∴.
由题意可知,D在以B为圆心,BD长为半径的圆上运动,
∵E为AD的中点,
∴E在以BA中点为圆心,长为半径的圆上运动,
CE的最大值即C到BA中点的距离加上长.
∵,,BC=2,
∴C到BA中点的距离即,
又∵,
∴CE的最大值即.
故答案为3.
10.如图,在矩形ABCD中,对角线AC,BD相交于点O,,,点F沿线段AO从点A至点O运动,连接DF,以DF为边作等边三角形DFE,点E和点A分别位于DF两侧,连接OE.现给出以下结论:
①;②;③直线;④点E运动的路程是.
其中正确的结论是______.(写出所有正确结论的序号)
【答案】①②③
【详解】解:①∵∠DAC=60°,OD=OA,
∴△OAD为等边三角形,
∴∠DOA=∠DAO=∠ODA=60°,AD=OD,
∵△DFE为等边三角形,
∴∠EDF=∠EFD=∠DEF=60°,DF=DE,
∵∠BDE+∠FDO=∠ADF+∠FDO=60°,
∴∠BDE=∠ADF,
∵∠ADF+∠AFD+∠DAF=180°,
∴∠ADF+∠AFD=180°﹣∠DAF=120°,
∵∠EFC+∠AFD+∠DFE=180°,
∴∠EFC+∠AFD=180°﹣∠DFE=120°,
∴∠ADF=∠EFC,
∴∠BDE=∠EFC,
故结论①正确;
②如图,连接OE,
在△DAF和△DOE中,
,
∴△DAF≌△DOE(SAS),
∴∠DOE=∠DAF=60°,
∵∠COD=180°﹣∠AOD=120°,
∴∠COE=∠COD﹣∠DOE=120°﹣60°=60°,
∴∠COE=∠DOE,
在△ODE和△OCE中,
,
∴△ODE≌△OCE(SAS),
∴ED=EC,∠OCE=∠ODE,
故结论②正确;
③∵∠ODE=∠ADF,
∴∠ADF=∠OCE,即∠ADF=∠ECF,
故结论③正确;
④如图,延长OE至,使=OD,连接,
∵△DAF≌△DOE,∠DOE=60°,
∴点F在线段AO上从点A至点O运动时,点E从点O沿线段运动到,
∵=OD=AD=AB•tan∠ABD=4•tan30°= ,
∴点E运动的路程是,
故结论④错误.
故答案为①②③.
11.如图,已知,平面内点P到点O的距离为2,连接AP,若且,连接AB,BC,则线段BC的最小值为__________.
【答案】
【详解】解:如图所示,延长PB到D使得PB=DB,
∵,
∴,
又∵∠APB=60°,
∴△APD是等边三角形,
∵B为PD的中点,
∴AB⊥DP,即∠ABP=90°,
∴∠BAP=30°,
以AO为斜边在AC下方作Rt△AMO,使得∠MAO=30°,连接CM,过点M作MH⊥AC于H,
∴,
同理可得,
∵∠OAM=30°=∠PAB,
∴∠BAM=∠PAO,
又∵,
∴△AMB∽△AOP,
∴,
∵点P到点O的距离为2,即OP=2,
∴,
∴点B在以M为圆心,以为半径的圆上,
连接CM交圆M(半径为)于,
∴当M、B、C三点共线时,即点B在点的位置时,BC有最小值,
∵AC=2AO=8,
∴AO=4,
∴,
∴,,
∴,
∴,
∴,
∴BC的最小值为,
故答案为:.
12.如图,线段为的直径,点在的延长线上,,,点是上一动点,连接,以为斜边在的上方作Rt,且使,连接,则长的最大值为__________.
【答案】
【详解】解:如图,作,使得,,则,,,
,,
,
,
,
,
即(定长),
点是定点,是定长,
点在半径为1的上,
,
的最大值为,
故答案为:.
三、解答题
13.如图,过抛物线上一点A作轴的平行线,交抛物线于另一点B,交轴于点C,已知点A的横坐标为.
(1)求抛物线的对称轴和点B的坐标;
(2)在AB上任取一点P,连结OP,作点C关于直线OP的对称点D;
①连接BD,求BD的最小值;
②当点D落在抛物线的对称轴上,且在轴上方时,求直线PD的函数表达式.
【答案】(1)对称轴为直线x=4;B(10,5).(2)①.②.
【详解】解:(1)把x=-2代入,得
,
∴A(﹣2,5),对称轴为直线x=﹣=4,
∵A、B关于对称轴对称,
∴B(10,5).
(2)①如图1中,
由题意点D在以O为圆心OC为半径的圆上,
∴当O、D、B共线时,BD的最小值=OB﹣OD=.
②如图2中,
图2
当点D在对称轴上时,在Rt△ODE中,OD=OC=5,OE=4,
∴DE==3,
∴点D的坐标为(4,3).
设PC=PD=x,在Rt△PDK中,,
∴x=,
∴P(,5),
设直线PD的解析式为y=kx+b,由题意得
,
∴,
∴直线PD的解析式为.
14.如图①,在中,,,D是BC的中点.
小明对图①进行了如下探究:在线段AD上任取一点P,连接PB,将线段PB绕点P按逆时针方向旋转,点B的对应点是点E,连接BE,得到.小明发现,随着点P在线段AD上位置的变化,点E的位置也在变化,点E可能在直线AD的左侧,也可能在直线AD上,还可能在直线AD的右侧.请你帮助小明继续探究,并解答下列问题:
(1)当点E在直线AD上时,如图②所示.
① ;②连接CE,直线CE与直线AB的位置关系是 .
(2)请在图③中画出,使点E在直线AD的右侧,连接CE,试判断直线CE与直线AB的位置关系,并说明理由.
(3)当点P在线段AD上运动时,求AE的最小值.
【答案】(1)①50;②;(2);(3)AE的最小值.
【详解】(1)①如图②中,
∵,,
∴,
②结论:.
理由:∵,,
∴,
∴,
∴,
∵AE垂直平分线段BC,
∴,
∴,
∵,,
∴,
∴,
∴.
故答案为50,.
(2)如图③中,以P为圆心,PB为半径作⊙P.
∵AD垂直平分线段BC,
∴,
∴,
∵,
∴ .
(3)如图④中,作于H,
∵点E在射线CE上运动,点P在线段AD上运动,
∴当点P运动到与点A重合时,AE的值最小,此时AE的最小值.
15.如图,等边三角形ABC的边长为4,点D是直线AB上一点.将线段CD绕点D顺时针旋转60°得到线段DE,连结BE.
(1)若点D在AB边上(不与A,B重合)请依题意补全图并证明AD=BE;
(2)连接AE,当AE的长最小时,求CD的长.
【答案】(1)见解析;(2)
【详解】解:(1)补全图形如图1所示,AD=BE,理由如下:
∵△ABC是等边三角形,
∴AB=BC=AC,∠A=∠B=60°,
由旋转的性质得:∠ACB=∠DCE=60°,CD=CE,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴AD=BE.
(2)如图2,过点A作AF⊥EB交EB延长线于点F.
∵△ACD≌△BCE,
∴∠CBE=∠A=60°,
∴点E的运动轨迹是直线BE,
根据垂线段最短可知:当点E与F重合时,AE的值最小,
此时CD=CE=CF,
∵∠ACB=∠CBE=60°,
∴AC∥EF,
∵AF⊥BE,
∴AF⊥AC,
在Rt△ACF中,
∴CF===,
∴CD=CF=.
16.如图所示,在中,,点是上一点,以为一边向右下方作等边,当由点运动到点时,求点运动的路径长.
【答案】点运动的路径长为.
【详解】点为定点,
可以看作是绕点顺时针旋转60°而来,
点运动的路径长等于点运动的路径长,即为的长,
,,
.
点运动的路径长为.
17.在平面直角坐标系中,A(a,0)、B(b,0),且a,b满足,C、D两点分别是y轴正半轴、x轴负半轴上的两个动点;
(1)如图1,若C(0,4),求△ABC的面积;
(2)如图1,若C(0,4),BC=5,BD=AE,且∠CBA=∠CDE,求D点的坐标;
(3)如图2,若∠CBA=60°,以CD为边,在CD的右侧作等边△CDE,连接OE,当OE最短时,求A,E两点之间的距离.
【答案】(1)△ABC的面积为12;(2)D点的坐标为(-2,0);(3)A,E两点之间的距离为
【详解】解:(1)∵,
∴,
由非负性可知,,解得:,
∴,,,
∵,
∴,
∴;
(2)由(1)知,,
∴,
∵,
∴,
在和中,
∴,
∴,
∵,,
∴,
在和中,
∴,
∴,
∵,,
∴,,
∴,
∴,
∵,
∴;
(3)由(2)可知CB=CA,
∵∠CBA=60°,
∴△ABC为等边三角形,∠BCA=60°,∠DBC=120°,
∵△CDE为等边三角形,
∴CD=CE,∠DCE=60°,
∵∠DCE=∠DCB+∠BCE,∠BCA=∠BCE+∠ECA,
∴∠DCB=∠ECA,
在△DCB和△ECA中,
∴,
∴,
∵,
∴,即:随着D点的运动,点E在过点A且平行于BC的直线PQ上运动,
∵要使得OE最短,
∴如图所示,当OE⊥PQ时,满足OE最短,此时∠OEA=90°,
∵,,
∴,,
∵,
∴,
∴,
∴当OE最短时,A,E两点之间的距离为.
18.如图,在矩形ABCD中,AB=3,AD=4,连接BD,将△ABD绕点D顺时针旋转,记旋转后的三角形为△A′B′D,旋转角为α(0°<α<360°且α≠180°).
(1)在旋转过程中,当A′落在线段BC上时,求A′B的长;
(2)连接A′A、A′B,当∠BA′B'=90°时,求tan∠A′AD;
(3)在旋转过程中,若△DAA′的重心为G,则CG的最小值=___________.
【答案】(1)4;(2)tan∠A′AD=3或;(3)
【详解】(1)解:(1)如图1,∵四边形ABCD矩形,AB=3,AD=4,
∴CD=AB=3,BC=AD=4,∠C=90°,
当A′落在线段BC上时,由旋转得A′D=AD=4,
∴A′C,
∴A′B=BC﹣A′C=4,
∴A′B的长为4.
(2)(2)如图2,点B′与点C在直线BD的同侧,作A′E⊥AD于点E,则∠A′EA=90°,
由旋转得∠B′A′D=∠BAD=90°,A′D=AD=4,
∵∠BA′B'=90°,
∴∠B′A′D+∠BA′B'=180°,
∴点B、A′、D在同一条直线上,
∵∠A′ED=∠BAD=90°,
∴BD5,
∴sin∠ADB,cos∠ADB,
∴A′EA′D4,EDA′D4,
∴AE=AD﹣ED=4,
∴tan∠A′AD3;
如图3,点B′与点C在直线BD的异侧,作A′E⊥AD交AD的延长线于点E,则∠E=90°,
由旋转得∠B′A′D=∠BAD=90°,A′D=AD=4,
∵∠BA′B'=90°,
∴∠B′A′D=∠BA′B',
∴A′D与A′B重合,
∴点B、A′、D在同一条直线上,
∵∠EDA′=∠ADB,
∴sin∠EDA′=sin∠ADB,cos∠EDA′=cos∠ADB,
∴A′EA′D,EDA′D,
∴AE=AD+ED=4,
∴tan∠A′AD,
综上所述,tan∠A′AD=3或.
(3)(3)如图4,在AD上截取DF,则,
作DH⊥AA′于点H,在DH上截取DGDH,连接FG、CG,则,
∵A′D=AD,
∴H为AA′的中点,
∴DH为△DAA′的中线,
∴点G为△DAA′的重心,
∵,∠FDG=∠ADH,
∴△DFG∽△DAH,
∴∠FGD=∠AHD=90°,
取DF的中点O,连接OC交⊙O于点P,连接OG,则OG=OP=ODDF,
∴点G在以点O为圆心、半径为的圆上运动,
∵CG+OG≥OC,即CG+OG≥CP+OP,
∴CGCP,∴CG≥CP,
∴当CG=CP时,CG的长最小,
∵OC,
∴CP=OC﹣OP,
∴CG的最小值是,
故答案为:.
19.如图所示,在矩形中,,,为的中点,为上一动点,为的中点,连接,求的最小值.
【答案】的最小值为.
【详解】解:如图:
当点F与点C重合时,点P在P1处,CP1=DP1,
当点F与点E重合时,点P在P2处,EP2=DP2,
∴P1P2∥CE且P1P2=CE.
当点F在EC上除点C、E的位置处时,有DP=FP.
由中位线定理可知:P1P∥CE且P1P=CF.
∴点P的运动轨迹是线段P1P2,
∴当BP⊥P1P2时,PB取得最小值.
∵矩形ABCD中,AB=4,AD=2,E为AB的中点,
∴△CBE、△ADE、△BCP1为等腰直角三角形,CP1=2.
∴∠ADE=∠CDE=∠CP1B=45°,∠DEC=90°.
∴∠DP2P1=90°.
∴∠DP1P2=45°.
∴∠P2P1B=90°,即BP1⊥P1P2,
∴BP的最小值为BP1的长.
在等腰直角BCP1中,CP1=BC=2,
∴BP1=
∴PB的最小值是.
故答案是:.
20.如图所示,在扇形中,,,点是上的动点,以为边作正方形,当点从点移动至点时,求点经过的路径长.
【答案】点经过的路径长为.
【详解】解:如图,由此BO交⊙O于F,取的中点H,连接FH、HB、BD.
易知△FHB是等腰直角三角形,HF=HB,∠FHB=90°,
∵∠FDB=45°=∠FHB,
∴点D在⊙H上运动,轨迹是(图中红线),
易知∠HFG=∠HGF=15°,
∴∠FHG=150°,
∴∠GHB=120°,易知HB=3,
∴点D的运动轨迹的长为=2π.
21.如图1,在中,,,,以点为圆心,为半径作圆.点为上的动点,连接,作,使点落在直线的上方,且满足,连接,.
(1)求的度数,并证明;
(2)如图2,若点在上时,连接,求的长;
(3)点在运动过程中,是否有最大值或最小值?若有,请求出当取得最大值或最小值时,的度数;若没有,请说明理由.
【答案】(1)见解析;(2);(3)有.① 当取得最大值时,;②当取得最小值时,.
【详解】(1)在中,,,
,
,
,,
,
,
,
,
;
(2)由(1)知,,
,
,
,
,,
,
,
,
在中,,,
由勾股定理得;
(3)有.由(1)知,,
,
,
是定值,
点是在以点为圆心,半径为的圆上,
①如图所示,当点在的延长线上时,取得最大值,
.
,
.
当取得最大值时,;
②如图所示,当点在线段上时,取得最小值,
,
,
当取得最小值时,.
22.如图所示,为等腰直角三角形,,直角顶点在第二象限,点在轴上移动,以为斜边向上作等腰直角,我们发现直角顶点点随着点的移动也在一条直线上移动,求这条直线的函数解析式.
【答案】直线的函数解析式为.
【详解】如图所示.当与轴平行时,过点作轴于点,过点作轴于点,交于点,
是等腰直角三角形,点的坐标是,
,
,
又是等腰直角三角形,
,,
点的坐标为.
当与原点重合时,在轴上,
此时,即,
设所求直线解析式为:,
将、代入得
解
直线的函数解析式为.
23.如图所示,点,的半径为2,,,点是上的动点,点是的中点,求的最小值.
【答案】的最小值为.
【详解】解:如图所示,连接交于点,连接,,
,
由勾股定理得:,
,,
.
当最小时,最小
当运动到时,最小.
此时的最小值为.
24.如图所示,在等腰中,,点在以斜边为直径的半圆上,为的中点,当点沿半圆从点运动至点时,求点运动的路径长.
【答案】点运动的路径长为.
【详解】解:如图所示,取的中点,的中点,的中点,连接、、、、、,
在等腰中,,
.
.
为的中点,
.
.
点在以为直径的圆上,
当点与点重合时,点与点重合:当点与点重合时,点与点重合,易得四边形为正方形,,
点运动的路径为以为直径的半圆.
点运动的路径长为.
25.如图1,已知在平面直角坐标系中,四边形是矩形点分别在轴和轴的正半轴上,连结,,,是的中点.
(1)求OC的长和点的坐标;
(2)如图2,是线段上的点,,点是线段上的一个动点,经过三点的抛物线交轴的正半轴于点,连结交于点
①将沿所在的直线翻折,若点恰好落在上,求此时的长和点的坐标;
②以线段为边,在所在直线的右上方作等边,当动点从点运动到点时,点也随之运动,请直接写出点运动路径的长.
【答案】(1) OC=,点的坐标为;(2) ①点的坐标为,②.
【详解】(1) ∵,
∴.
∵四边形是矩形,
∴.
∵是的中点,
∴,
∴点的坐标为.
(2) ①∵,
∴,
∴.
设将翻折后,点落在上的处,
则,
∴,
∴,
∴.
∵,
∴.
∵,
∴,
∵,
∴.
∴.
∴,∴点的坐标为.
②动点P在点O时,
∵抛物线过点P(0,0)、
求得此时抛物线解析式为y=
∴E(,0),
∴直线DE: ,
∴F1(3,);
当动点P从点O运动到点M时,
∵抛物线过点
求得此时抛物线解析式为,
∴E(6,0),
∴直线DE:y=-
∴F2(3,)
∴点F运动路径的长为,
∵△DFG为等边三角形,
∴G运动路径的长为
26.在等边三角形中,点D为上一点,连接,将绕D逆时针旋转角度得到,连接,已知,;
(1)如图1,若,,连接,求的长;
(2)如图2,若,分别取的中点H,的中点F,连接,,求证:;
(3)如图3,若,P为上一点,且满足,连接,将沿着所在直线翻折得到,连接,当最大时,直接写出的面积.
【答案】(1);(2)见解析;(3).
【详解】(1)解:由旋转性质可知,,
∵旋转角,
∴是等边三角形,则,,
∵为等边三角形,
∴,,
∴,即,
∴(SAS),
∴,
∵,,,
∴,,
又∵,
∴,
∴;
(2)证明:延长,使,连接,,则,
即为的中点,
∵为的中点,
∴为的中位线,即,
旋转角,由旋转性质可知:,
∵为的中点,
∴,平分,
∴,,则,
∴为等边三角形,
∴,,
又∵为等边三角形,
∴,,
∴,即,
∴(SAS),
∴,即,
∵为的中点,
∴,
,
∴
∴.
(3)由(1)知,,,,
∵,则,
∴,
由,得,
作,则:,
∴,则,,,
即点的轨迹为:以为圆心,为半径的圆,
由翻折可知,,而,当,,在同一直线上时取最大值,即:取最大值,如图
此时,,,
则.
27.在菱形中,,是对角线上的一点,连接.
(1)当在的中垂线上时,把射线绕点顺时针旋转后交于,连接.如图①,若,求的长.
(2)在(1)的条件下,连接,把绕点顺时针旋转得到如图②,连接,点为的中点,连接,求的最大值.
【答案】(1) (2)
【详解】(1)解:过点F作于点M,如下图:
∵四边形ABCD是菱形,且
∴
∵为菱形对角线
∴,
又∵在的中垂线上
∴
∴
∴,
在中,
∴
设:,则
∵ 即: 解得:
∴
∵,
∴
∴
∴
又∵
∴
∴
∴
∴
(2)连接AC,延长AE交BC于点M,则有,点H的运动轨迹是以点B为圆心,BH为半径的圆,因为点C为固定点,点N为CH的中点,所以点N的运动轨迹是以点M为圆心,NM为半径的圆,如下图:
此时:在在,,当 A、M、N三点共线时,AN最大
则:在中,
∵
∴
∴
又∵M点是BC的中点,N是CH的中点
∴
∴
28.在中,D为直线上一动点,连接,将绕点B逆时针旋转,得到,连接与相交于点F.
(1)如图1,若D为的中点,,,,连接,求线段的长;
(2)如图2,G是线段延长线上一点,D在线段上,连接,,若,,,,证明;
(3)如图3,若为等边三角形,,点M为线段上一点,且,点P是直线上的动点,连接,,,请直接写出当最小时的面积.
【答案】(1);(2)证明见解析;(3).
【详解】(1)解:∵为的中点,,,
∴,则由勾股定理,可得:,
作,交于,
由题意可知,,,
∴,,
∴,
又∵,
∴(AAS),
∴,,
则,
由勾股定理可得:;
(2)证明:由旋转可知,为等腰直角三角形,
∴,,,
∵,
∴,
又∵,,
∴,,
又∵,
∴,
在和中,,
∴(AAS),
∴,,
则:,
∵,
∴,即:,
∴,
又∵,
由三角形内角和定理可得:,
即:,
∴,
作,交延长线于,连接,
∴为等腰直角三角形,
∴,,,
∵,
∴,
∴四边形是平行四边形,
∴,即,
∴;
(3)作,交于,
∵是等边三角形,
∴,,平分,
则,
将绕点逆时针旋转,则,,
∴,
∴(SAS),
∴
∴,
作点关于的对称点,连接,,由对称易知,,
∴
当最小时,即最小,亦即、、在同一直线,且,如图:
作,交于,则,
∴,,
∵,,
∴,,四边形是矩形,
则,,即,
由轴对称可知,,
∴是等边三角形,则:,
∵,
∴,,
∴,,
则由勾股定理可得:,,
∵,,
则为,之间的距离,
∴,即的高
∴,
∴.
题型06 最值问题之瓜豆原理-备战2024年中考数学重难点专题最后冲刺之最值问题(全国通用): 这是一份题型06 最值问题之瓜豆原理-备战2024年中考数学重难点专题最后冲刺之最值问题(全国通用),文件包含题型06最值问题之瓜豆原理原卷版docx、题型06最值问题之瓜豆原理解析版docx等2份试卷配套教学资源,其中试卷共69页, 欢迎下载使用。
题型04 最值问题之隐圆-备战2024年中考数学重难点专题最后冲刺之最值问题(全国通用): 这是一份题型04 最值问题之隐圆-备战2024年中考数学重难点专题最后冲刺之最值问题(全国通用),文件包含题型04最值问题之隐圆原卷版docx、题型04最值问题之隐圆解析版docx等2份试卷配套教学资源,其中试卷共44页, 欢迎下载使用。
题型01 最值问题之将军饮马-备战2024年中考数学重难点专题最后冲刺之最值问题(全国通用): 这是一份题型01 最值问题之将军饮马-备战2024年中考数学重难点专题最后冲刺之最值问题(全国通用),文件包含题型01最值问题之将军饮马-中考数学重难点专题最后冲刺之最值问题全国通用原卷版docx、题型01最值问题之将军饮马-中考数学重难点专题最后冲刺之最值问题全国通用解析版docx等2份试卷配套教学资源,其中试卷共53页, 欢迎下载使用。












