
专题28二次函数与角压轴问题-中考数学压轴大题之经典模型培优案(全国通用)
展开中考数学压轴大题之经典模型培优案
专题28二次函数与角压轴问题
经典例题
【例1】(2022·山东菏泽·统考中考真题)如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A−2,0、B8,0两点,与y轴交于点C0,4,连接AC、BC.
(1)求抛物线的表达式;
(2)将△ABC沿AC所在直线折叠,得到△ADC,点B的对应点为D,直接写出点D的坐标.并求出四边形OADC的面积;
(3)点P是抛物线上的一动点,当∠PCB=∠ABC时,求点P的坐标.
【答案】(1)y=−14x2+32x+4
(2)D−8,8,24
(3)P6,4或343,−1009
【分析】(1)直接利用待定系数法求抛物线解析式即可;
(2)先利用勾股定理的逆定理证明△ABC为直角三角形,再根据折叠的性质得出点B、C、D三点共线,继而通过证明△DBE∼△CBO,利用相似三角形的性质即可得出点D的坐标,根据四边形OADC的面积=S△ADC+S△AOC=S△ABC+S△AOC进行求解即可;
(3)分两种情况讨论:当点P在x轴上方时,当点P在x轴下方时,分别求解即可.
【详解】(1)将A−2,0,B8,0,C0,4代入抛物线y=ax2+bx+c(a≠0),得
0=4a−2b+c0=64a+8b+c4=c,解得a=−14b=32c=4,
所以,抛物线的表达式为y=−14x2+32x+4;
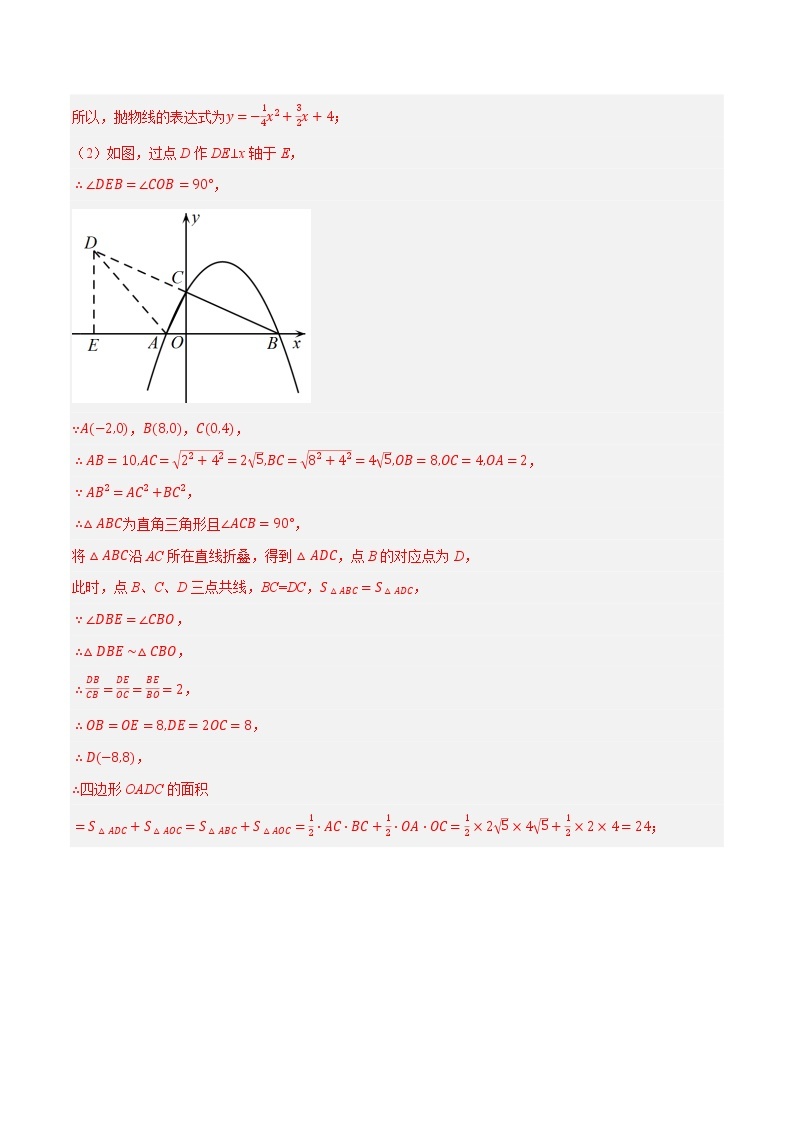
(2)如图,过点D作DE⊥x轴于E,
∴∠DEB=∠COB=90°,
∵A−2,0,B8,0,C0,4,
∴AB=10,AC=22+42=25,BC=82+42=45,OB=8,OC=4,OA=2,
∵AB2=AC2+BC2,
∴△ABC为直角三角形且∠ACB=90°,
将△ABC沿AC所在直线折叠,得到△ADC,点B的对应点为D,
此时,点B、C、D三点共线,BC=DC,S△ABC=S△ADC,
∵∠DBE=∠CBO,
∴△DBE∼△CBO,
∴DBCB=DEOC=BEBO=2,
∴OB=OE=8,DE=2OC=8,
∴D−8,8,
∴四边形OADC的面积
=S△ADC+S△AOC=S△ABC+S△AOC=12⋅AC⋅BC+12⋅OA⋅OC=12×25×45+12×2×4=24;
(3)
当点P在x轴上方时,
∵∠PCB=∠ABC,
∴CP∥x轴,
∴点P的纵坐标为4,即4=−14x2+32x+4,
解得x=6或0(舍去)
∴P6,4;
当点P在x轴下方时,设直线CP交x轴于F,
∵∠PCB=∠ABC,
∴CF=BF,
设OF=t,则CF=BF=8−t,
在Rt△COF中,由勾股定理得OC2+OF2=CF2,
即42+t2=8−t2,
解得t=3,
∴F3,0,
∵C0,4,
∴设直线CF的解析式为y=kx+4,
即0=3k+4,解得k=−43,
∴直线CF的解析式为y=−43x+4,
令−43x+4=−14x2+32x+4,解得x=343或0(舍去),
当x=343时,y=−14×3432+32×343+4=−1009
∴P343,−1009;
综上,P6,4或343,−1009.
【点睛】本题考查了二次函数的综合题目,涉及待定系数法求二次函数解析式,勾股定理的逆定理,折叠的性质,相似三角形的判定和性质,求一次函数的解析式,等腰三角形的性质等知识,熟练掌握知识点并能够灵活运用是解题的关键.
【例2】(2022·江苏苏州·统考中考真题)如图,在二次函数y=−x2+2mx+2m+1(m是常数,且m>0)的图像与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.其对称轴与线段BC交于点E,与x轴交于点F.连接AC,BD.
(1)求A,B,C三点的坐标(用数字或含m的式子表示),并求∠OBC的度数;
(2)若∠ACO=∠CBD,求m的值;
(3)若在第四象限内二次函数y=−x2+2mx+2m+1(m是常数,且m>0)的图像上,始终存在一点P,使得∠ACP=75°,请结合函数的图像,直接写出m的取值范围.
【答案】(1)A(-1,0);B(2m+1,0);C(0,2m+1);∠OBC=45°
(2)m=1
(3)0
【分析】(1)分别令x,y等于0,即可求得A,B,C的坐标,根据OC=OB,∠BOC=90°,即可求得∠OBC=45°;
(2)方法一:如图1,连接AE.由解析式分别求得DF=m+12,OF=m,BF=m+1.根据轴对称的性质,可得AE=BE,由tan∠ACE=AECE=BECE=BFOF=m+1m,建立方程,解方程即可求解.方法二:如图2,过点D作DH⊥BC交BC于点H.由方法一,得DF=m+12,BF=EF=m+1.证明△AOC∽△DHB,根据相似三角形的性质建立方程,解方程即可求解;
(3)设PC与x轴交于点Q,当P在第四象限时,点Q总在点B的左侧,此时∠CQA>∠CBA,即∠CQA>45°.
【详解】(1)当y=0时,−x2+2mx+2m+1=0.
解方程,得x1=−1,x2=2m+1.
∵点A在点B的左侧,且m>0,
∴A−1,0,B2m+1,0.
当x=0时,y=2m+1.
∴C0,2m+1.
∴OB=OC=2m+1.
∵∠BOC=90°,
∴∠OBC=45°.
(2)方法一:如图1,连接AE.
∵y=−x2+2mx+2m+1=−x−m2+m+12,
∴Dm,m+12,Fm,0.
∴DF=m+12,OF=m,BF=m+1.
∵点A,点B关于对称轴对称,
∴AE=BE.
∴∠EAB=∠OCB=45°.
∴∠CEA=90°.
∵∠ACO=∠CBD,∠OCB=∠OBC,
∴∠ACO+∠OCB=∠CBD+∠OBC,
即∠ACE=∠DBF.
∵EF∥OC,
∴tan∠ACE=AECE=BECE=BFOF=m+1m.
∴m+1m=m+12m+1.
∵m>0,
∴解方程,得m=1.
方法二:如图2,过点D作DH⊥BC交BC于点H.
由方法一,得DF=m+12,BF=EF=m+1.
∴DE=m2+m.
∵∠DEH=∠BEF=45°,
∴DH=EH=22DE=22m2+m,
BE=2BF=2m+1.
∴BH=BE+HE=22m2+3m+2.
∵∠ACO=∠CBD,∠AOC=∠BHD=90°,
∴△AOC∽△DHB.
∴OAOC=DHBH.
∴12m+1=22m2+m22m2+3m+2,即12m+1=mm+2.
∵m>0,
∴解方程,得m=1.
(3)0
∵∠ACQ=75°,
∴∠CAO<60°.
∴tan∠CAO<3,
∵OC=2m+1,
∴2m+1<3.
解得m<3−12,
又m>0,
∴0
【点睛】本题考查了二次函数综合,求二次函数与坐标轴的交点,角度问题,解直角三角形,相似三角形的性质,三角形内角和定理,综合运用以上知识是解题的关键.
【例3】(2022·天津·统考二模)已知抛物线y=x2+6x+5与x轴交于点A,B(点A在点B左侧),顶点为D,且过C(-4,m).
(1)求点A,B,C,D的坐标;
(2)点P在该抛物线上(与点B,C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求△PBC的面积的最大值,
②连接BD,当∠PCB=∠CBD时,求点P的坐标.
【答案】(1)A(-5,0),B(-1,0);C(-4,-3);D(-3,-4)
(2)①278;②(0,5)或(−32,−74)
【分析】(1)把抛物线解析式化为顶点式即可求出点D的坐标,令y=0,求出x的值即可得到A、B的坐标,把x=-4代入抛物线解析式求出y即可求出点C的坐标;
(2)①先求出直线BC的解析式为y=x+1,过点P作PE⊥x轴于E交BC于F,则点P的坐标为(t,t2+6t+5),点F的坐标为(t,t+1),PF=−t2−5t−4,再根据S△PBC=S△PFC+S△PFB =−32t+522+278,进行求解即可;②分如图1所示,当点P在直线BC上方时,如图2所示,当点P在直线BC下方时,两种情况讨论求解即可.
(1)
解:∵抛物线解析式为y=x2+6x+5=x+32−4,
∴抛物线顶点D的坐标为(-3,-4);
令y=0,则x2+6x+5=0,
解得x=−1或x=−5,
∵抛物线y=x2+6x+5与x轴交于点A,B(点A在点B左侧),
∴点A的坐标为(-5,0),点B的坐标为(-1,0);
令x=−4,则y=−42+6×−4+5=−3,
∴点C的坐标为(-4,-3);
(2)
解:①设直线BC的解析式为y=kx+b,
∴−k+b=0−4k+b=−3,
∴k=1b=1,
∴直线BC的解析式为y=x+1,
过点P作PE⊥x轴于E交BC于F,
∵点P的横坐标为t,
∴点P的坐标为(t,t2+6t+5),点F的坐标为(t,t+1),
∴PF=t+1−t2−6t−5=−t2−5t−4,
∴S△PBC=S△PFC+S△PFB
=12PF⋅xP−xC+12PF⋅xB−xP
=12PF⋅xB−xC
=−32t2+5t+4
=−32t+522+278,
∴当t=−52时,△PBC的面积最大,最大为278;
②如图1所示,当点P在直线BC上方时,
∵∠PCB=∠CBD,
∴PC∥BD,
设直线BD的解析式为y=k1x+b1,
∴−k1+b1=0−3k1+b1=−4,
∴k1=2b1=2,
∴直线BD的解析式为y=2x+2,
∴可设直线PC的解析式为y=2x+b2,
∴2×−4+b2=−3,
∴b2=5,
∴直线PC的解析式为y=2x+5,
联立y=2x+5y=x2+6x+5得x2+4x=0,
解得x=0或x=−4(舍去),
∴y=5,
∴点P的坐标为(0,5);
如图2所示,当点P在直线BC下方时,设BD与PC交于点M,
∵点C坐标为(-4,-3),点B坐标为(-1,0),点D坐标为(-3,-4),
∴BC2=−4−−12+−32=18,BD2=−3−−12+−42=20,CD2=−4−−32+−3−−42=2,
∴BC2+CD2=BD2,
∴∠BCD=90°,
∴∠BCM+∠DCM=90°,∠CBD+∠CDB=90°,
∵∠CBD=∠PCB,
∴MC=MB,∠MCD=∠MDC,
∴MC=MD,
∴MD=MB,
∴M为BD的中点,
∴点M的坐标为(-2,-2),
设直线CP的解析式为y=k2x+b3,
∴−4k2+b3=−3−2k2+b3=−2,
∴k2=12b3=−1,
∴直线CP的解析式为y=12x−1,
联立y=12x−1y=x2+6x+5得2x2+11x+12=0,
解得x=−32或x=−4(舍去),
∴y=−74,
∴点P的坐标为(−32,−74);
综上所述,当∠PCB=∠CBD时,点P的坐标为(0,5)或(−32,−74);
【点睛】本题主要考查了二次函数综合,一次函数与几何综合,二次函数的性质,待定系数法求函数解析式,勾股定理的逆定理,等腰三角形的性质与判定等等,正确作出辅助线,利用分类讨论的思想求解是解题的关键.
【例4】(2022·四川达州·统考中考真题)如图1,在平面直角坐标系中,已知二次函数y=ax2+bx+2的图象经过点A(−1,0),B(3,0),与y轴交于点C.
(1)求该二次函数的表达式;
(2)连接BC,在该二次函数图象上是否存在点P,使∠PCB=∠ABC?若存在,请求出点P的坐标:若不存在,请说明理由;
(3)如图2,直线l为该二次函数图象的对称轴,交x轴于点E.若点Q为x轴上方二次函数图象上一动点,过点Q作直线AQ,BQ分别交直线l于点M,N,在点Q的运动过程中,EM+EN的值是否为定值?若是,请求出该定值;若不是,请说明理由.
【答案】(1)y=−23x2+43x+2
(2)P2,2或285,−28625
(3)163
【分析】(1)待定系数法求解析式即可求解;
(2)根据题意,分情况讨论,①过点C作关于x=1的对称点P,即可求P的坐标,②x轴上取一点D,使得DC=DB,则∠DCB=∠ABC,设Dd,0,根据勾股定理求得CD,BD,建列方程,解方程求解即可;
(3)设Qt,−23t2+43t+2,−1
∴C0,2,
∵过点A(−1,0),B(3,0),
设二次函数的表达式为y=ax+1x−3 =ax2−2x−3,
将点C0,2代入得,
2=−3a,
解得a=−23,
∴y=−23x2+43x+2,
(2)∵二次函数y=ax2+bx+2的图象经过点A(−1,0),B(3,0),
∴抛物线的对称轴为x=1,
①如图,过点C作关于x=1的对称点P,
∴CP∥AB,
∴∠PCB=∠ABC,
∵C0,2,
∴P2,2,
②x轴上取一点D,使得DC=DB,则∠DCB=∠ABC,设Dd,0,
则CD=22+d2,BD=3−d,
∴22+d2=3−d2,
解得d=56,
即D56,0,
设直线CD的解析式为y=kx+b,
56k+b=0b=2,
解得k=−125b=2,
∴直线CD的解析式为y=−125x+2,
联立y=−125x+2y=−23x2+43x+2,
解得x=0y=2或x=285y=−28625,
∴P285,−28625,
综上所述,P2,2或285,−28625,
(3)EM+EN的值是定值163,
设Qt,−23t2+43t+2,−1
∵A−1,0,B3,0,E1,0,Ft,0,
∴AE=BE=2,AF=t+1,BF=3−t,
∴ME∥QF,NE∥QF,
∴△AME∽△AQF,△BNE∽△BQF,
∴MEQF=AEAF,NEQF=BEBF,
即MEQF=2t+1,NEQF=23−t,
∴ME=2t+1QF,NE=23−tQF,
∴ME+NE=2t+1+23−tQF,
∵QF=−23t2+43t+2=−23×t+1t−3,
∴ME+NE=2t+1+23−t×−23×t+1t−3
=−43t−3−t+1
=163.
即EM+EN的值是定值163
【点睛】本题考查了二次函数综合,待定系数法求解析式,角度问题,相似三角形的性质与判定,掌握二次函数的性质是解题的关键.
【例5】.(2022·湖北黄石·统考中考真题)如图,抛物线y=−23x2+23x+4与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.
(1)A,B,C三点的坐标为____________,____________,____________;
(2)连接AP,交线段BC于点D,
①当CP与x轴平行时,求PDDA的值;
②当CP与x轴不平行时,求PDDA的最大值;
(3)连接CP,是否存在点P,使得∠BCO+2∠PCB=90°,若存在,求m的值,若不存在,请说明理由.
【答案】(1)A−2,0;B3,0;C0,4
(2)①15;②940
(3)存在点P,m=74
【分析】(1)令x=0,则y=4,令y=0,则−23x2+23x+4=0,所以x=-2或x=3,由此可得结论;
(2)①由题意可知,P(1,4),所以CP=1,AB=5,由平行线分线段成比例可知,PDDA=CPAB=15.
②过点P作PQ∥AB交BC于点Q,所以直线BC的解析式为:y=-43x+4.设点P的横坐标为m,则P(m,-23m2+23m+4),Q(12m2−12m,-23m2+23m+4).所以PQ=m-(12m2−12m)=-12m2+32m,因为PQ∥AB,所以PDDA=PQAB=−12m2+32m5=−110(m−32)2+940,由二次函数的性质可得结论;
(3)假设存在点P使得∠BCO+2∠BCP=90°,即0<m<3.过点C作CF∥x轴交抛物线于点F,由∠BCO+2∠PCB=90°,可知CP平分∠BCF,延长CP交x轴于点M,易证△CBM为等腰三角形,所以M(8,0),所以直线CM的解析式为:y=-12x+4,令−23x2+23x+4=-12x+4,可得结论.
【详解】(1)解:令x=0,则y=4,
∴C(0,4);
令y=0,则−23x2+23x+4=0,
∴x=-2或x=3,
∴A(-2,0),B(3,0).
故答案为:(-2,0);(3,0);(0,4).
(2)解:①∵CP∥x轴,C0,4,
∴P1,4,CP=1,AB=5
又∵CP∥x轴,
∴△CPD∽△BAD
∴PDDA=CPAB=15;
②过P作PQ∥AB交BC于点Q,
设直线BC的解析式为y=k1x+b1,
把B(3,0),C(0,4)代入,得
3k1+b1=0b1=4,解得k1=−43b1=4,
∴直线BC的解析式为y=−43x+4,
设Pm,−23m2+23m+4,则Q12m2−12m,−23m2+23m+4,
∴PQ=m−12m2−12m=−12m2+32m,
∵PQ∥AB,
∴△QPD∽△BAD
∴PDDA=PQAB=−12m2+32m5=−110m−322+940,
∴当m=32时,PDDA取最大值940;
(3)解:假设存在点P使得∠BCO+2∠BCP=90°,即0
∴∠FCP=∠BMC,
∵∠BCO+2∠BCP=90°,
∴CP平分∠BCF,
∴∠BCP=∠FCP,
∴∠BCP=∠BMC,
∴BC=BM,
∴△CBM为等腰三角形,
∵BC=5,
∴BM=5,OM=8,M8,0,
设直线CM解析式为y=kx+b,
把C(0,4),M8,0代入,得
8k+b=0b=4,解得:k=−12b=4,
∴直线CM的解析式为y=−12x+4,
联立y=−12x+4y=−23x2+23x+4,
解得x=74或x=0(舍),
∴存在点P满足题意,即m=74.
【点睛】此题是二次函数综合题,主要考查了待定系数法,平行线分线段成比例,角度的存在性等相关内容,解本题的关键是求抛物线解析式,确定点P的坐标.
培优训练
一、解答题
1.(2022·四川绵阳·东辰国际学校校考模拟预测)如图,以△ABC的边AB和AB边上高所在直线建立平面直角坐标系,已知AB=4,C0,−3,tan∠CAB+tan∠CBA=4,抛物线y=ax2+bx+c经过A,B,C三点.
(1)求抛物线解析式.
(2)点G是x轴上一动点,过点G作GH⊥x轴交抛物线于点H,抛物线上有一点Q,若以C,G,Q,H为顶点的四边形为平行四边形,求点G的坐标.
(3)点P是抛物线上的一点,当∠PCB=∠ACO时,求点P的坐标.
【答案】(1)y=x2−2x−3
(2)G的坐标为1+103,0或1−103,0
(3)当∠PCB=∠ACO时,点P的坐标为(4,5)或52,−74
【分析】(1)先求出OC=3,再根据正切的定义得到1OA+1OB=43,结合OA+OB=4求出A−1,0,B3,0,再利用待定系数法求出对应的函数解析式即可;
(2)先证明只存在以GH为对角线的平行四边形,设Gn,0,Qm,m2−2m−3,则Hn,n2−2n−3,根据平移的特点建立方程3n2−2n−3=0进行求解即可;
(3)先求出∠OBC=45°,BC=2OC=32,如图②,作∠P1CB=∠ACO,过点B作BD1⊥BC交CP1于点D1,过点D1作D1M⊥x轴于点M,可得△BMD1为等腰直角三角形,BM=D1M=22D1B,再由tan∠P1CB=tan∠ACO=OAOC=13,得到BM=D1M=22D1B=1,则点D1的坐标为2,1,求出直线CD1的解析式为y=2x−3,联立y=2x−3y=x2−2x−3,可得P1的坐标为4,5.如图②,延长D1B至D2,使得D1B=D2B,连接CD2交抛物线于点P2,过点D2作D2N⊥x轴于点N,则D24,−1,求出直线CD2的解析式为y=12x−3,联立y=12x−3y=x2−2x−3,可得点P2的坐标为52,−74.
【详解】(1)解:∵C0,−3,
∴OC=3,
∵tan∠CAB+tan∠CBA=4,
∴OCOA+OCOB=4,
∴1OA+1OB=43,
由1OA+1OB=43OA+OB=4,
可得OA⋅OB=3OA+OB=4,
解得OA=1OB=3或OA=3OB=1(舍去),
∴A−1,0,B3,0,
将A−1,0,B3,0,C0,−3代入y=ax2+bx+c可得a−b+c=09a+3b+c=0c=−3,
解得a=1b=−2c=−3,
∴抛物线解析式为y=x2−2x−3.
(2)解:如图①,∵GH∥y轴,点Q在抛物线上,
∴以GH为边的平行四边形不存在,只存在以GH为对角线的平行四边形,
设Gn,0,Qm,m2−2m−3,则Hn,n2−2n−3,
由点的平移可得m−n=n−0m2−2m−3−0=n2−2n−3−−3,消元整理可得3n2−2n−3=0,解得n1=1+103,n2=1−103,
∴点G的坐标为1+103,0或1−103,0.
(3)解:∵OC=OB=3,
∴∠OBC=45°,BC=2OC=32,
如图②,作∠P1CB=∠ACO,过点B作BD1⊥BC交CP1于点D1,过点D1作D1M⊥x轴于点M,
∴∠D1BM=45°,
∴△BMD1为等腰直角三角形,BM=D1M=22D1B,
∵tan∠P1CB=tan∠ACO=OAOC=13,
∴D1BBC=D1B32=13,D1B=2,
∴BM=D1M=22D1B=1,
∴点D1的坐标为2,1,
由D12,1,C0,−3可得直线CD1的解析式为y=2x−3,
联立y=2x−3y=x2−2x−3,
解得x1=0y1=−3(舍去),x2=4y2=5,
∴P1的坐标为4,5.
如图②,延长D1B至D2,使得D1B=D2B,连接CD2交抛物线于点P2,过点D2作D2N⊥x轴于点N,
∴D24,−1,
由D24,−1,C0,−3可得直线CD2的解析式为y=12x−3,
联立y=12x−3y=x2−2x−3,
解得x1=0y1=−3(舍去),x2=52y2=−74,
∴点P2的坐标为52,−74.
综上可得当∠PCB=∠ACO时,点P的坐标为4,5或52,−74.
【点睛】本题主要考查了二次函数综合,一次函数与几何综合,平行四边形的性质,等腰直角三角形的性质与判断,解直角三角形等等,灵活运用所学知识并利用数形结合的思想求解是解题的关键.
2.(2022·山东日照·校考一模)如图,抛物线y=ax2+bx+3与x轴交于A1,0,B3,0两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)如图2,M是抛物线x轴下方的抛物线上一点,连接MO、MB、MC,若△MOC的面积是△MBC面积的3倍,求点M的坐标
(3)如图3,连接AC、BC,在抛物线上是否存在点N(不与点A重合),使得∠BCN=∠ACB?若存在求出点N的横坐标,若不存在说明理由
【答案】(1)y=x2−4x+3;
(2)83,−59
(3)抛物线上存在一点N,使得∠BCN=∠ACB,点N的坐标是113,169
【分析】(1)利用待定系数法即可求得抛物线的解析式;
(2)先用待定系数法求出直线BC的解析式为y=−x+3,设点M的坐标是m,m2−4m+3,过点M作直线MP∥y轴交BC于点N,则点P的是m,−m+3,求出MP=−m2+3m,得到S△MOC=32m,S△MBC=−32m2+92m,根据△MOC的面积是△MBC面积的3倍,列方程求得m的值,即可求得点M的坐标;
(3)抛物线上存在一点N,使得∠BCN=∠ACB,过点B作BE⊥AB交CN于点E,则∠EBO=90°,证明△ABC≌△EBCASA得到BE=AB=2,求出点E的坐标是3,2,待定系数法求出直线CN的解析式,联立直线CN的解析式与抛物线的解析式即可求出点N的坐标.
【详解】(1)解:把A1,0,B3,0代入y=ax2+bx+3得,
a+b+3=09a+3b+3=0,
解得a=1b=−4,
∴抛物线的解析式为y=x2−4x+3;
(2)如图,
对于y=x2−4x+3,
当x=0时,y=3,
∴点C的坐标为0,3,
设直线BC的解析式为y=kx+t,代入B3,0,C0,3得,
3k+t=0t=3,解得k=−1t=3,
∴直线BC的解析式为y=−x+3,
设点M的坐标是m,m2−4m+3,过点M作直线MP∥y轴交BC于点N,
则点P的是m,−m+3,
∴MP=−m+3−m2−4m+3=−m2+3m,
∵A1,0,B3,0,C0,3,
∴S△MOC=12OC·m=32m,S△MBC=12MP·OB=−32m2+92m,AB=2,
∵△MOC的面积是△MBC面积的3倍,
∴32m=3−32m2+92m,
解得m=0(不合题意,舍去)或m=83,
当m=83时,m2−4m+3=832−4×83+3=−59,
∴点M的坐标是83,−59;
(3)抛物线上存在一点N,使得∠BCN=∠ACB,过点B作BE⊥AB交CN于点E,则∠EBO=90°,
∵B3,0,C0,3,
∴OB=OC,
∴△OBC是等腰直角三角形,
∴∠OBC=45°,
∴∠OBC=∠EBC=45°,
∵BC=BC,∠BCN=∠ACB,
∴△ABC≌△EBCASA,
∴BE=AB=2,
∴点E的坐标是3,2,
设直线CN的解析式为y=mx+n,代入E3,2,C0,3得,
3m+n=2n=3,解得m=−13n=3,
∴直线CN的解析式为y=−13x+3,
联立y=x2−4x+3与y=−13x+3得,
y=−13x+3y=x2−4x+3,
解得x=113y=169或x=0y=3(不合题意,舍去),
∴抛物线上存在一点N,使得∠BCN=∠ACB,点N的坐标是113,169.
【点睛】此题是二次函数综合题,主要考查了利用待定系数法求函数解析式、二次函数与一次函数的交点问题、全等三角形的判定和性质等知识,关键是添加合适的辅助线解决问题.
3.(2021·贵州遵义·校考模拟预测)如图,直线y=−x+3与x轴、y轴分别交于B、C两点,抛物线y=−x2+bx+c经过点B、C的,与x轴另一交点为A,顶点为D.
(1)求抛物线的解析式;
(2)在抛物线对称轴是否存在一点E,使得△BCE是等腰三角形,若存在,求出E的点坐标,若不存在,请说明理由;
(3)在抛物线的对称轴上是否存在一点P,使得∠APB=∠OCB?若存在,求出点P的坐标,若不存在,请说明理由.
【答案】(1)y=−x2+2x+3
(2)1,14或1,−14或1,3−17或1,3+17或1,1
(3)1,2+22或1,−2−22
【分析】(1)先求出B、C坐标,然后把B、C坐标代入抛物线解析式中求解即可;
(2)设点E的坐标为1,m,则BC2=18,BE2=m2+4,CE2=m2−6m+10,再分三种情况:当BC=BE,当BC=CE,当BE=CE讨论求解即可;
(3)如图所示,当点P在x轴上方时,过点B作BF⊥AP于F,先证明△PBF是等腰直角三角形,则可设BF=PF=a,则PA=PB=2a,进而得到a2+2−12a2=16,求出PH=2+22得到点P的坐标,利用对称性求出点P在x轴下方时的坐标即可得到答案.
【详解】(1)解:∵直线y=−x+3与x轴、y轴分别交于B、C两点,
∴B3,0,C0,3,
把B3,0,C0,3代入抛物线解析式y=−x2+bx+c中得:
−9+3b+c=0c=3,
∴b=2c=3,
∴抛物线解析式为y=−x2+2x+3;
(2)解:∵抛物线解析式为y=−x2+2x+3=−x−12+4,
∴抛物线对称轴为直线x=1,
设点E的坐标为1,m,
∴BC2=32+33=18,BE2=3−12+0−m2=m2+4,CE2=1−02+m−32=m2−6m+10,
当BC=BE时,则m2+4=18,
解得m=±14,
∴点E的坐标为1,14或1,−14;
当BC=CE时,则m2−6m+10=18,
解得m=3+17或m=3−17,
∴点E的坐标为1,3−17或1,3+17;
当BE=CE时,则m2+4=m2−6m+10,
解得m=1,
∴点E的坐标为1,1;
综上所述,点E的坐标为1,14或1,−14或1,3−17或1,3+17或1,1;
(3)解:如图所示,当点P在x轴上方时,过点B作BF⊥AP于F,
∵OB=OC=3,∠BOC=90°,
∴∠APB=∠OCB=45°,
∴△PBF是等腰直角三角形,
∴可设BF=PF=a,则PA=PB=2a,
∴AF=PA−PF=2−1a,
由对称性可知A−1,0,
∴AB=4,
∴a2+2−12a2=16,
∴a2=8+42,
∴PB2=16+82,
∴PH=PB2−BH2=12+82=2+22,
∴P1,2+22;
∴由对称性可知当点P在x轴下方时,点P的坐标为1,−2−22;
综上所述,点P的坐标为1,2+22或1,−2−22
【点睛】本题主要考查了二次函数综合,待定系数法求函数解析式,勾股定理,等腰三角形的定义,等腰直角三角形的性质与判定等等,熟知相关知识是解题的关键.
4.(2022·湖南长沙·长沙市南雅中学校联考一模)已知二次函数y=ax2+bx−32(a≠0)的图象经过A(1,0)、B(−3,0)两点,顶点为点C.
(1)求二次函数的解析式;
(2)如二次函数y=ax2+bx−32的图象与y轴交于点G,抛物线上是否存在点Q,使得∠QAB=∠ABG,若存在求出Q点坐标,若不存在请说明理由;
(3)经过点B并且与直线AC平行的直线BD与二次函数y=ax2+bx−32图象的另一交点为D,DE⊥AC,垂足为E,DF∥y轴交直线AC于点F,点M是线段BC之间一动点,FN⊥FM交直线BD于点N,延长MF与线段DE的延长线交于点H,点P为△NFH的外心,求点M从点B运动到点C的过程中,P点经过的路线长.
【答案】(1)y=12x2+x−32
(2)−4,52或−2,−32
(3)1
【分析】(1)将A(1,0)、B(-3,0)代入y=ax2+bx−32,即可求解;
(2)先求出BG的解析式为y=−12x−32,然后再进行分类讨论,分别求得点Q的坐标即可;
(3)可知△DNH与△FNH是直角三角形,外心P在斜边NH的中点,分别求出直线AC及直线BD的函数关系式,再分为当M运动到C点时及当点M运动到B点时两种情况进行讨论,求解即可.
【详解】(1)∵二次函数y=ax2+bx−32的图像经过A(1,0)、B(-3,0),
∴a+b−32=09a−3b−32=0,
解得a=12b=1,
∴二次函数的解析式为y=12x2+x−32;
(2)由题可知G点坐标0,−32,
设直线BG的解析式为y=px+q,得:
−3k+b=00k+b=−32,解得:k=−12b=−32,
∴BG的解析式为y=−12x−32,
①AQ∥BG,直线AQ的解析式y=−12x+12,
联立直线AQ与二次函数解析式y=−12x+12y=12x2+x−32 ,
解得x1=1y1=0或x2=−4y2=52
此时Q的坐标为−4,52,
②直线y=−12x+12与y轴的交点为K0,12,其关于x轴的对称点为K10,−12
直线AK1的解析式为:y=12x−12 与二次函数解析式联立得
y=12x−12y=12x2+x−32,
解得x1=1y1=0或x2=−2y2=−32,
此时Q的坐标为−2,−32,
综上,抛物线上存在点Q使得∠QAB=∠BAG,Q点坐标为−4,52或−2,−32
(3)如图,易知△DNH与△FNH是直角三角形,外心P在斜边NH的中点,
∴PD=PF=12NH,所以点P是线段DF的垂直平分线上的动点,
∵直线AC的解析式为y=x-1,BD∥AC,
∴直线BD的解析式为y=x+3,
∴D(3,6),
①当M运动到C点时H1与点E重合,FN1⊥AC,则FN1⊥BD,又因为∠DEF=90°,DE=EF,
∴四边形DN1FE为正方形,
∴P1是线段DF的中点(3,4);
②当点M运动到B点时,FN2⊥FH2,
∵四边形DN1FE是正方形
∴∠N1FN2=∠BFC,∠N2N1F=∠BCF=90°,
∴△N2N1F∽△BCF,
∴CFN1F=BCN2N1,
∵四边形DN1FE是正方形,
∴N1(1,4),
∴BCN2N1=CFN1F=4222=2,
∴N1N2=2,
∴N2(2,5),
同理H2(6,3),
所以N2H2的中点P2(4,4),
∵P1(3,4),
∴P1P2=1
【点睛】本题考查二次函数的图象及性质,熟练掌握二次函数的图象及性质,会用待定系数法求函数的解析式,会求函数的交点坐标,根据点M的运动情况确定P点的轨迹是线段是解题的关键.
5.(2022·内蒙古包头·包头市第三十五中学校考三模)如图,抛物线y=ax2+bx+3交x轴于A(3,0),B(−1,0)两点,交y轴于点C.
(1)求抛物线的解析式和对称轴.
(2)若R为抛物线上一点,满足∠BCR=45°,求R的坐标.
(3)若点P在抛物线的对称轴上,点Q是平面直角坐标系内的任意一点,是否存在点P 使得A、C、P、Q为顶点的四边形是矩形,若存在,请直接写出所有符合条件的点Q的坐标,若不存在,请说明理由.
【答案】(1)y=−x2+2x+3,对称轴为直线x=1
(2)(4,-5)
(3)存在,(4,1)或(-2,1)或2,3+172或2,3−172
【分析】(1)利用待定系数解答,即可求解;
(2)过点B作BM⊥BC交CR于点M,过点M作ME⊥x轴于点E,证明△BOC≌△MBE,可得点E(2,-1),然后求出直线CR的解析式,再与抛物线解析式联立,即可求解;
(3)设P(1,t),点Q(m,n),分两种情况讨论:然后分两种情况讨论:当AC为边时,当AC为对角线时,即可求解.
【详解】(1)解:∵抛物线y=ax2+bx+3交x轴于A3,0,B−1,0两点,
∴9a+3b+3=0a−b+3=0,
解得:a=−1b=2,
∴该抛物线的解析式为y=−x2+2x+3=−x−12+4,
∴对称轴为直线x=1;
(2)解:当x=0时,y=3,
∴OC=3,
∵点B(-1,0),
∴OB=1,
如图,过点B作BM⊥BC交CR于点M,过点M作ME⊥x轴于点E,
∵∠BCR=45°,
∴△BCM为等腰直角三角形,∠CBO+∠EBM=90°,
∴BM=BC,
∵∠EBM+∠BME=90°,
∴∠CBO=∠BME,
∵∠BEM=∠BOC=90°,
∴△BOC≌△MBE,
∴EM=BO=1,BE=OC=3,
∴OE=2,
∴点E(2,-1),
设直线CR的解析式为y=kx+b1k≠0
把点C(0,3),M(2,-1)代入得:
b1=32k+b1=−1,解得:k=−2b1=3,
∴直线CR的解析式为y=−2x+3,
联立得:y=−x2+2x+3y=−2x+3,解得: 0x=4y=−5 或x=0y=3(舍去),
∴点R(4,-5);
(3)解:存在.
设P(1,t),点Q(m,n),
当以AC为边时,点C向点P(或点Q)平移的方向和距离与点A向点Q(或点P)平移的方向和距离相同,且AP=CQ(或AQ=CP),
∴0−1=3−m3−t=0−n1−32+t2=m2+n−32或0−m=3−13−n=0−t12+3−t2=m−32+n2,
解得:t=4m=4n=1 或t=−2m=−2n=1,
∴此时点Q的坐标为(4,1)或(-2,1)
如图,当AC为对角线时,AC=PQ,且PQ与AC的中点重合,如图,
PQ=AC=32+32=32,
∴1+m2=32n+t2=321−m2+n−t2=322,解得:n=3+172m=2t=3−172或n=3−172m=2t=3+172,
∴此时点Q的坐标为2,3+172或2,3−172;
综上所述,点Q的坐标为(4,1)或(-2,1)或2,3+172或2,3−172
【点睛】本题主要考查了二次函数的综合题,一次函数的图像和性质,矩形的性质,熟练掌握二次函数的综合题,一次函数的图像和性质,矩形的性质,利用数形结合思想解答是解题的关键,是中考的压轴题.
6.(2021·辽宁盘锦·统考二模)如图,在平面直角坐标系中,直线y=2x+4与x轴,y轴分别交于A,B两点,抛物线y=ax2+x+ca≠0经过A,B两点与x轴相交于点C点.
(1)求抛物线的解析式;
(2)点P在抛物线上,连接PB,当∠PBC+∠OBA=45°时,求点P的坐标;
(3)点M为抛物线上任意一点,当S△ABM:S△ABC=1:3时,请直接写出点M的坐标.
【答案】(1)y=−12x2+x+4
(2)6,−8和3,52
(3)M12,4,M2−4,−8
【分析】(1)先确定A、B两点的坐标,然后再运用待定系数法即可解答;
(2)先说明△OBC是等腰直角三角形,然后再分点P在x轴上方和下方两种情况解答即可;
(3)求得S△ABM=4,设点M的坐标为(m,n},再利用待定系数法求得直线AM的解析式,根据三角形面积公式列得方程求解即可.
(1)
解:∵y=2x+4
∴当y=0时,x=-2;当x=0时,y=4
∴A(-2,0),B(0,4)
将A(-2,0),B(0,4)代入y=ax2+x+c得
4a−2+c=0c=4,解得a=−12c=4
∴ 抛物线的解析式为:y=−12x2+x+4.
(2)
解:∵−12x2+x+4=0
∴x1=-2,x2=4
∴C(4,0)
∴OB=OC
∴△OBC是等腰直角三角形
①当点P在x轴下方时,设直线BP与x轴交于点D
∵ ∠PBC+∠OBD=∠OBC=45°
∠PBC+∠OBA=45°
∴ ∠OBD=∠OBA
∴ 点A,D关于y 轴对称
∴ D(2,0)
由B(0,4),D(2,0)可求直线BP解析式为:y=−2x+4
y=−2x+4y=−12x2+x+4
∴P1(6,−8)
②当点P在x轴上方时,设直线BP与x轴交于点E
∵ ∠OBC=45°,∠PBC+∠OBA=45°
∴ ∠PBA=90°
可证△OAB∽△OBE
∴OB2=OA⋅OE
∴ OE=8
∴ E(8,0)
由B(0,4),E(8,0)可求直线BP解析式为:y=−12x+4
y=−12x+4y=−12x2+x+4
∴P2(3,52)
综上,点P的坐标为6,−8和3,52.
(3)
解:由题意可得:A(-2,0),B(0,4),C(4,0)
∴AC=6
∴SΔABC=12AC×OB=12
∵S△ABM:S△ABC=1:3
∴S△ABM=4
设点M的坐标为(m,n)且n=−12m2+m+4
运用待定系数法可求得AM的解析式为:y=nm+2(x+2)=nm+2x+2nm+2
设直线AM与y轴交于N,则N(0,2nm+2)
∴BN=4−2nm+2
∴SΔABM=12|4−2nm+2|⋅|m+2|=4,整理得:|12m2+m|=4,
∴ 12m2+m=4或12m2+m=−4
解方程12m2+m=4得:m1=2,m2=−4
∴n=−12×22+2+4=4或n=−12×−42−4+4=−8
∴M12,4,M2−4,−8
对于方程12m2+m=−4,整理得m2+2m+8=0,
∵Δ=22−4×1×8=−28<0
∴没有实数解
∴M12,4,M2−4,−8.
【点睛】本题属于二次函数的综合题,主要考查了二次函数图像与一次函数图像相结合问题、相似三角形的判定和性质等知识点,解题的关键是掌握分类讨论以及学会利用参数构建方程解决问题.
7.(2022·贵州遵义·统考三模)已知,如图,抛物线与坐标轴相交于点A−1,0,C0,−3两点,对称轴为直线x=1,对称轴与x轴交于点D.
(1)求抛物线的解析式;
(2)点P是抛物线上的点,当∠ACP=45°时,求点P的坐标;
(3)点F为二次函数图像上与点C对称的点,点M在抛物线上,点N在抛物线的对称轴上,是否存在以点F,A,M,N为顶点的平行四边形?若存在,直接写出点M的坐标,若不存在,说明理由.
【答案】(1)y=(x−1)2−4
(2)P(4,5)
(3)M(0,−3)或M(−2,5)或M(4,5)
【分析】(1)由对称轴为直线x=1则设抛物线y=a(x−1)2+k代入点A、C的坐标求出解析式;
(2)过AC作AQ⊥AC,且AQ=AC,过A作MN∥y轴,过C作CN⊥MN于N,过Q作QM⊥MN于M,构建ΔMQA≅ΔNAC,即可得出Q(2,1),求得直线CQ的解析式为:yCQ=2x−3与抛物线解析式联立即可得出P点坐标;
(3)设N(1,n),M(m,m2−2m−3),分以AF为对角线时以AN为对角线时, 以AM为对角线时,进行讨论,列出方程组,即可解答问题.
【详解】(1)解:∵抛物线对称轴为直线x=1,
∴设抛物线y=a(x−1)2+k,
把A(−1,0),C(0,−3)代入y=a(x−1)2+k得:
{0=a×(−2)2+k−3=a×1+k,
∴{a=1k=−4,
∴y=(x−1)2−4;
(2)如图过AC作AQ⊥AC,且AQ=AC,过A作MN∥y轴,过C作CN⊥MN于N,过Q作QM⊥MN于M,
∴∠QMA=∠CNA=90∘,∠QAC=90∘,
∴∠1+∠2=90∘,∠1+∠3=90∘,
∴∠2=∠3,
∴ΔMQA≅ΔNAC,
∴MA=NC=1,MQ=AN=3,
∴Q(2,1),
设直线CQ的解析式为y=kx+b,
∴{−3=k×0+b1=2k+b,
∴{k=2b=−3,
∴yCQ=2x−3,
∴{y=2x−3y=(x−1)2−4,
∴{x1=0y1=−3,{x2=4y2=5,
∴P(4,5);
(3)∵y=(x−1)2−4,
∴y=x2−2x−3,
依题意设N(1,n),M(m,m2−2m−3),
∵C(0,−3),对称轴为直线x=1,
∴F(2,−3),
∵A(−1,0),F(2,−3),N(1,n),M(m,m2−2m−3),
当以AF为对角线时,{−1+2=1+m0+(−3)=n+(m2−2m−3),
∴m=0,
∴M(0,−3),
当以AN为对角线时,{−1+1=2+m0+n=−3+(m2−2m−3),
∴m=−2,
∴M(−2,5),
当以AM为对角线时,{−1+m=2+10+(m2−2m−3)=−3+n,
∴m=4,
∴M(4,5),
综上所述:M(0,−3)或M(−2,5)或M(4,5).
【点睛】此题考查了二次函数的图像和性质,一次函数的解析式求法,构造全等三角形的判定和性质,平行四边形存在性问题,是一道有关二次函数的综合题,掌握以上知识点是解题的关.
8.(2022·广东深圳·深圳市宝安第一外国语学校校考模拟预测)如图1,在平面直角坐标系中.抛物线y=ax2+bx+2与x轴交于A(−4,0)和B(1,0),与y轴交于点C,连接AC,BC.
(1)求该抛物线的解析式;
(2)如图2,点M为直线AC上方的抛物线上任意一点,过点M作y轴的平行线,交AC于点N,过点M作x轴的平行线,交直线AC于点Q,求△MNQ周长的最大值;
(3)点P为抛物线上的一动点,且∠ACP=45°−∠BAC,请直接写出满足条件的点P的坐标.
【答案】(1)y=−12x2−32x+2
(2)6+25
(3)−5,−3或−237,7549
【分析】(1)利用待定系数法解答,即可求解;
(2)先利用勾股定理求出AC=25,再求出直线AC解析式为:y=12x+2,设Mx,−12x2−32x+2,则Nx,12x+2,可得MN=−12x2−2x,再由△QMN∽△AOC,可得MQ=2MN,NQ=5MN,从而得到△MNQ周长=(3+5)MN,再利用二次函数的性质,即可求解;
(3)在x轴负半轴上取点E,使OE=OC,连接CE交抛物线于点P,可得∠ACP=45°−∠BAC,然后求出直线CE解析式为y=x+2,再求出直线CE与抛物线的交点坐标;作E关于直线AC的对称点F,连接CF并延长交抛物线于P′,连接EF交AC于点T,则∠ACP′=∠ACP,设Fm,n,根据AE=AF,CE=CF,可得F−145,85.再求出直线CF的解析式,即可求解.
(1)
解:把A(−4,0)和B(1,0)代入y=ax2+bx+2,得:
16a−4b+2=0a+b+2=0,解得a=−12b=−32,
∴抛物线解析式为y=−12x2−32x+2;
(2)
解:令y=0,则y=2,
∴C(0,2),
∴OC=2,
∵点A(-4,0),
∴OA=4,
∴AC=OA2+OC2=25,
∴可设直线AC解析式为y=kx+2,
把A(−4,0)代入得:−4k+2=0,
解得:k=12,
∴直线AC解析式为:y=12x+2,
设Mx,−12x2−32x+2,则Nx,12x+2,
∴MN=−12x2−32x+2−12x+2 =−12x2−2x,
∵MQ∥x轴,MN∥y轴,
∴∠MQN=∠CAO,∠NMQ=∠AOC=90°,
∴△QMN∽△AOC,
∴MNOC=MQOA=NQAC,即MN2=MQ4=NQ25,
∴MQ=2MN,NQ=5MN,
∴△MNQ周长MN+MQ+QN=MN+2MN+5MN =(3+5)MN
=(3+5)×−12x2−2x=−3+52(x+2)2+6+25
∵−3+52<0,
∴当x=−2时,△MNQ周长最大值为6+25.
(3)
解:在x轴负半轴上取点E,使OE=OC,连接CE交抛物线于点P,如图.
∴OE=2,
∴E−2,0,∠CEO=45°,
此时∠ACP=45°−∠BAC,即P是满足条件的点.
∵C0,2,E−2,0,
∴可设直线CE解析式为y=k1x+2,
把点E(-2,0)代入得:
−2k1+2=0,解得:k1=1,
∴直线CE解析式为y=x+2,
联立y=x+2y=−12x2−32x+2,解得:x1=0y1=2(舍去)或x=−5y=−3
∴此时点P(−5,−3)
∴P(−5,−3);
作E关于直线AC的对称点F,连接CF并延长交抛物线于P′,连接EF交AC于点T,则∠ACP′=∠ACP,
∴P′是满足条件的点,
设Fm,n,
根据对称性得:AE=AF,CE=CF,
∴m+42+n2=−4+22m2+n−22=0+22+2−02
解得m=−143n=85或m=−2n=0(舍去),
∴F−145,85.
∵F−145,85,C0,2
∴可设直线CF解析式为y=k2x+2,
把点F−145,85,代入得:−145k2+2=85,
解得:k2=17,
∴直线CF解析式为y=17x+2,
联立y=17x+2y=−12x2−32x+2,解得x=0y=2或x=−237y=7549,
∴P′−237,7549,
综上,P′为−5,−3或−237,7549.
【点睛】本题是二次函数的综合题,熟练掌握二次函数的图象和性质,相似三角形的判定和性质,二次函数与一次函数的交点问题,利用数形结合思想解答是解题的关键.
9.(2022·江苏无锡·模拟预测)如图,直线l:y=−3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2−2ax−3a(a<0)经过点B.
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′,将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l'与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数).
【答案】(1)y=−x2+2x+3
(2)S=−12(m−52)2+258,最大值为258
(3)45°
【分析】(1)利用直线l的解析式求出B点坐标,再把B点坐标代入二次函数解析式即可求出a的值;
(2)设M的坐标为(m,-m2+2m+3),然后根据面积关系将△ABM的面积进行转化;
(3)由(2)可知m=52,代入二次函数解析式即可求出纵坐标的值;可将求d1+d2最大值转化为求AC的最小值.
(1)
解:令x=0代入y=-3x+3,
∴y=3,
∴B(0,3),
把B(0,3)代入y=ax2−2ax−3a,
∴3=-3a,
∴a=-1,
∴二次函数解析式为:y=-x2+2x+3;
(2)
令y=0代入y=-x2+2x+3,
∴0=-x2+2x+3,
∴x=-1或3,
∴抛物线与x轴的交点横坐标为-1和3,
∵M在抛物线上,且在第一象限内,
∴0<m<3,
令y=0代入y=-3x+3,
∴x=1,
∴A的坐标为(1,0),
由题意知:M的坐标为(m,-m2+2m+3),
S=S四边形OAMB-S△AOB
=S△OBM+S△OAM-S△AOB
=12×m×3+12×1×(-m2+2m+3)-12×1×3
=-12(m-52)2+258
∴当m=52时,S取得最大值258.
(3)
由(2)可知:M′的坐标为(52,74);
过点M′作直线l1∥l′,过点B作BF⊥l1于点F,
根据题意知:d1+d2=BF,
此时只要求出BF的最大值即可,
∵∠BFM′=90°,
∴点F在以BM′为直径的圆上,
设直线AM′与该圆相交于点H,
∵点C在线段BM′上,
∴F在优弧BM′H上,
∴当F与M′重合时,
BF可取得最大值,
此时BM′⊥l1,
∵A(1,0),B(0,3),M′(52,74),
∴由勾股定理可求得:AB=10,M′B=554,M′A=854,
过点M′作M′G⊥AB于点G,
设BG=x,
∴由勾股定理可得:M′B2-BG2=M′A2-AG2,
∴8516−(10−x)2=12516−x2,
∴,x=5108, cos∠M′BG=BGM′B=22,
∵l1∥l′,
∴∠BCA=90°,
∠BAC=45°.
【点睛】本题考查二次函数的综合问题,涉及待定系数求二次函数解析式,求三角形面积,圆的相关性质等知识,内容较为综合,学生需要认真分析题目,化动为静去解决问题.
10.(2022·黑龙江齐齐哈尔·统考三模)如图,二次函数y=−x2+c的图象交x轴于点A、点B,其中点B的坐标为(2,0),点C的坐标为(0,2),过点A、C的直线交二次函数的图象于点D.
(1)求二次函数和直线AC的函数表达式;
(2)连接DB,则△DAB的面积为________;
(3)在y轴上确定点Q,使得∠AQB=135°,点Q的坐标为________;
(4)点M是抛物线上一点,点N为平面上一点,是否存在这样的点N,使得以点A、点D、点M、点N为顶点的四边形是以AD为边的矩形?若存在,请你直接写出点N的坐标;若不存在,请说明理由.
【答案】(1)y=−x2+4;y=x+2
(2)6
(3)(0,22−2)或(0,2−22)
(4)存在,N1(−3,1)或N2(6,−2)
【分析】(1)把B点坐标代入函数解析式即可求出二次函数解析式,求出A点坐标后即可求出AC解析式;
(2)先求出D点坐标,再用公式法求△DAB的面积;
(3)当Q在正半轴时,根据C点坐标可得∠CAB=45°,根据二次函数对称性结合∠AQB=135°可得∠QAO=22.5°=12∠CAO,即AQ平分∠CAO,即可求出Q点坐标;当Q在负半轴时根据对称性可求;
(4)以AD为矩形边长时,分别过A、D作直线AD的垂线;当AD为对角线时根据矩形的对角线互相平分且相等求值即可.
【详解】(1)∵二次函数y=−x2+c的图象过点B(2,0),
∴0=−22+c,解得c=4
∴二次函数解析式为y=−x2+4
∴A点坐标为(-2,0)
设直线AC的解析式为y=kx+b
∴0=−2k+b2=b,解得:k=1b=2
∴直线AC的解析式为y=x+2
(2)∵直线AC:y=x+2与二次函数交于点A、D
∴联立y=−x2+4y=x+2,解得x=−2y=0或x=1y=3
∴D点坐标为:(1,3)
∵AB=4
∴S△DAB=12AB×yD=12×3×4=6
(3)∵C(0,2),A点坐标为(-2,0)
∴∠CAB=45°
当Q在正半轴时,
∵∠AQB=135°,QA=QB
∴∠QAO=22.5°=12∠CAO
∴AQ平分∠CAO
过Q作PQ⊥AC于P
设OQ=x,则OQ=PQ=x,CQ=2PQ=2x
∴OC=OQ+CQ=2x+x=2
解得x=22−2
∴Q点坐标为(0,22−2)
当Q在与轴负半轴时,根据对称性可得Q点坐标为(0,2−22)
∴Q点坐标为(0,2−22)或(0,22−2)
(4)当AD是矩形边长时
过A作AM⊥AD交抛物线于M
∵直线AC的解析式为y=x+2
∴设直线AM的解析式为y=−x+b1
代入A点(-2,0)得b1=−2
∴直线AM的解析式为y=−x−2
∴联立y=−x2+4y=−x−2,解得x=−2y=0或x=3y=−5
∴M点坐标为(3,−5)
∵此时MN平行且等于AD
∴由A(-2,0)平移到D(1,3)与由M(3,−5)平移到N的平移方式一致
∴N点坐标为(6,−2)
同理::过D作DM⊥AD交抛物线于M,此时M(0,4),N(-3,1)
综上所述,存在,N点坐标为(6,−2)或(-3,1)
【点睛】本题考查二次函数与几何综合,熟练掌握二次函数的图象及性质,函数图象平移的性质,矩形的判定,分类讨论是解题的关键.
11.(2022·山东泰安·统考二模)如图,在平面直角坐标系中,直线y=12x+2与x轴交于点A,与y轴交于点C,抛物线y=−12x2+bx+c经过A、C两点,与x轴的另一交点为点B.
(1)求抛物线的函数表达式;
(2)点D为直线AC上方抛物线上一动点,
①连接BC、CD,设直线BD交线段AC于点E,求DEEB的最大值;
②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF中的∠DCF=2∠BAC,若存在,求出点D的坐标;若不存在,请说明理由.
【答案】(1)y=−12x2−32x+2
(2)①45;②存在,D(-2,3)
【分析】(1)根据题意得到A(-4,0),C(0,2)代入y=-12x2+bx+c,于是得到结论;
(2)①如图1,令y=0,解方程得到x1=-4,x2=1,求得B(1,0),过D作DM⊥x轴于M,过B作BN⊥x轴交于AC于N,根据相似三角形的性质即可得到结论;②根据勾股定理的逆定理得到△ABC是以∠ACB为直角的直角三角形,取AB的中点P,求得P(-32,0),得到PA=PC=PB=52,过D作x轴的平行线交y轴于R,交AC的延线于G,解直角三角形即可得到结论.
(1)
解:对于函数:y=12x+2,
令x=0,则y=2,令y=0,则x=-4,
∴A(-4,0),C(0,2),
∵抛物线y=-12x2+bx+c经过A.C两点,
∴0=−12×16−4b+c2=c,
∴b=-32,c=2,
∴y=-12x2-32x+2;
(2)
解:①如图,令y=0,
∴−12x2−32x+2=0,
∴x1=−4,x2=1,
∴B(1,0),
过D作DM⊥x轴交AC于点M,过B作BN⊥x轴交于AC于N,
∴DM∥BN,
∴△DME∽△BNE,
∴DEBE=DMBN,
设Da,−12a2−32a+2,
∴Ma,12a+2,
∵B(1,0),
∴N1,52,
∴DEBE=DMBN=−12a2−2a52=−15a+22+45,
∵-15<0,
∴当a=-2时,DEBE的最大值是45;
②∵A(-4,0),B(1,0),C(0,2),
∴AC=25,BC=5,AB=5,
∴AC2+BC2=AB2,
∴△ABC是以∠ACB为直角的直角三角形,取AB的中点P,
∴P−32,0,
∴PA=PC=PB=52,
∴∠CPO=2∠BAC,
∴tan∠CPO=tan2∠BAC=43,
过D作x轴的平行线交y轴于R,交AC的延长线于G,如图,
∴∠DCF=2∠BAC=∠DGC+∠CDG,
∴∠CDG=∠BAC,
∴tan∠CDG=tan∠BAC=12,即RCDR=12,
令Da,−12a2−32a+2,
∴DR=-a,RC=−12a2−32a,
∴−12a2−32a−a=12,
∴a1=0(舍去),a2=−2,
∴xD=−2,yD=3.
∴D(-2,3).
【点睛】本题考查了二次函数综合题,涉及待定系数法求函数的解析式,相似三角形的判定和性质,解直角三角形,直角三角形的性质等知识点,正确的作出辅助线是解题的关键.
12.(2022·湖南岳阳·统考二模)如图1,直线y=2x+2交x轴于点A,交y轴于点C,过A、C两点的抛物线y=ax2+32x+c与x轴的另一交点为B.
(1)求该抛物线的函数表达式;
(2)如图2,点D是抛物线在第一象限内的一点,连接OD,将线段OD绕O逆时针旋转90°得到线段OM,过点M作MN∥x轴交直线AC于点N.求线段MN的最大值及此时点D的坐标;
(3)在(2)的条件下,若点E是点A关于y轴的对称点,连接DE,试探究在抛物线上是否存在点P,使得∠PED=45°?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=−12x2+32x+2
(2)最大值为3;D2,3
(3)存在,P11+6,62,P20,2
【分析】(1)根据直线解析式求得A,C的坐标,然后代入抛物线解析式,待定系数法求解析式即可求解;
(2)令Dt,−12t2+32t+2,将线段OD绕O逆时针旋转90°得到线段OM,得M12t2−32x−2,t,Nt−22,t,进而得出MN=−12t−22+3,根据二次函数的性质求解即可求解;
(3)分2种情形讨论,①当点P在点D右侧时,过D作DQ⊥DE,交EP的延长线与点Q,过D作直线l∥x轴,过E作EM⊥l于M,过Q作QN⊥l于N,证明△EDM≌△DQN,求得Q的坐标,进而求得直线EQ的解析式为:y=12x−12,联立抛物线解析式,即可求得点P的坐标,②②当点P在点D左侧时,同①方法求解即可.
(1)
解:在直线y=2x+2中,令y=0得x=−1,则A−1,0,
令x=0得y=2,则C0,2,
由题意得:a−32+c=0c=2 ,
解得:a=−12c=2,
∴y=−12x2+32x+2,
(2)
令Dt,−12t2+32t+2,
∵将线段OD绕O逆时针旋转90°得到线段OM ,
M12t2−32x−2,t,
∵MN∥x轴且点N在直线y=2x+2上,
∴Nt−22,t,
∴MN=t−22−12t2−32t−2=−12t2+2t+1=−12t−22+3,
∴当t=2时,MNmax=3,
此时D2,3,
(3)
①当点P在点D右侧时,
过D作DQ⊥DE,交EP的延长线与点Q,
∵∠PED=45°,
∴DE=DQ,
过D作直线l∥x轴,过E作EM⊥l于M,过Q作QN⊥l于N,
∴∠EMD=∠DNQ=90°,
∴∠1+∠2=90°,
∵DQ⊥DE,
∴∠2+∠3=90°,
∴∠1=∠3 ,
∴△EDM≌△DQN,
∴DN=EM=3,QN=DM=1,
∴Q5,2,
∵点E是点A关于y轴的对称点,A−1,0,
∴ E1,0,
设直线EQ的解析式为:y=kx+b,代入Q5,2,E1,0,得
kx+b=05k+b=1,
解得k=12b=12,
∴直线EQ的解析式为:y=12x−12,
令−12x2+32x+2=12x−12,
解得:x1=1+6,x2=1−6(舍去) ,
∴P11+6,62,
②当点P在点D左侧时,
过D作DR⊥DE,交EP的延长线与点R,
∵∠PED=45°,
∴DE=DR,
过D作直线ℎ∥y轴,过E作EH⊥ℎ于H,过R作RG⊥ℎ于G,
同理可证:△EDH≌△DRG,
∴RG=DH=3,DG=EH=1,
∴R=−1,4,
即可得直线RE的解析式为:y=−2x+2,
令−12x2+32x+2=−2x+2,
解得:x1=0,x2=7(舍去),
∴P20,2,
综上所述:P11+6,62,P20,2.
【点睛】本题考查了二次函数综合问题,求一次函数解析式,一次函数与二次函数交点,全等三角形的性质与判定,二次函数的性质,二次函数最值,综合运用以上知识是解题的关键.
13.(2022·山东泰安·统考三模)如图1,已知二次函数C1:y=ax2+bx+ca≠0的图像与x轴交于点A−1,0,B(4,0)两点,与y轴交于点C,OC=4,如图1
(1)求二次函数C1的表达式:
(2)将C1沿x轴对称,再沿x轴正方向向右平移2个单位长度,得到新抛物线C2,直线MN⊥x轴,分别交C1,C2于点M,N,如图2,求线段MN的最大值:
(3)在抛物线C1上是否存在点P,使得∠BOP=∠BCO−∠ACO?若存在,求出P的横坐标;若不存在,请说明理由.
【答案】(1)y=x2−3x−4
(2)212
(3)存在,9+1815或6+2345
【分析】(1)待定系数法求解析式;
(2)根据题意求得C2的解析式,设Mm,−m2+7m−6,则Nm,m2−3m−4,求得MN的表达式,根据二次函数的性质求得最值即可;
(3)如图,作A关于y轴的对称点A′,则A′1,0,∠ACO=∠A′CO.∠BCA'=∠OCB−∠ACO.连接A′C,作A'H⊥BC于H,等面积法求得A′H,勾股定理求得CH,作BM⊥BO使得A′HCH=BMBO,证明△MBO∽△AHC,可得∠MPB=∠A′CO=∠ACO=∠BOP,代入已知值,得BM=125,求得M的坐标,进而求得直线OM的表达式为y=35x,联立抛物线解析式,即可求得P的横坐标,根据对称性,联立y=−35x和y=x2−3x−4即可求得另一个点P的横坐标.
(1)
解:如图1
∵二次函数C1:y=ax2+bx+ca≠0的图像与x轴交于点A−1,0,B(4,0)两点,与y轴交于点C,OC=4,
∴C0,−4,
设抛物线解析式为y=ax+1x−4,代入C0,−4,得−4=−4a,
解得a=1,
∴y=x+1x−4=x2−3x−4,
∴二次函数C1的表达式y=x2−3x−4,
(2)
将C1:y=x2−3x−4沿x轴对称,
得到y=−x2+3x+4,
再沿x轴正方向向右平移2个单位长度,得到新抛物线C2,
则C2:y=−x−22+3x−2+4=−x2+7x−6,
∵直线MN⊥x轴,分别交C1,C2于点M,N,
设Mm,−m2+7m−6,则Nm,m2−3m−4
∴MN=−m2+7m−6−m2−3m−4
=−2m2+10m−2
=−2m−522+212,
∴MN的最大值为212,
(3)
(3)如图,作A关于y轴的对称点A′,则A′1,0,
∴∠ACO=∠A′CO.
∴∠BCA'=∠OCB−∠ACO.
连接A′C,作A'H⊥BC于H,
∵A−1,0,则A′1,0,
∵B4,0,
∴A′B=3,
∵OC=4,
∴ S△A′BC=12A′B⋅OC=6,BC=42.
∴ A′H=612×42=322,
∴ CH=A′C2−A′H2=522,
作BM⊥BO使得A′HCH=BMBO,
∵∠MBO=∠AHC=90°
∴△MBO∽△AHC
∴∠MPB=∠A′CO=∠ACO=∠BOP
则322522=BM4,得BM=125,
∴M4,125,
设直线OM的表达式为y=kx,代入M4,125,
得k=1254=35,
∴直线OM的表达式为y=35x,
由y=35x和y=x2−3x−4联立解得,
x1=9+1815,x2=9−1815.
∵13<181<14,∴9−181<0,
∴x2不合题意,舍去,
∴点P的横坐标为9+1815,
由y=−35x和y=x2−3x−4联立解得,x=6±2345(负值舍去).
∴点P的横坐标为9+1815或6+2345.
【点睛】本题考查了轴对称的性质,相似三角形的性质与判定,根据对称性转化角是解题的关键.
14.(2022·江苏镇江·统考二模)如图所示,抛物线y=−x2+bx+3经过点B(3,0),与x轴交于另一点A,与y轴交于点C.
(1)求抛物线所对应的函数表达式;
(2)如图,设点D是x轴正半轴上一个动点,过点D作直线l⊥x轴,交直线BC于点E,交抛物线于点F,连接AC、FC.
①若点F在第一象限内,当∠BCF=∠BCA时,求点F的坐标;
②若∠ACO+∠FCB=45°,则点F的横坐标为______.
【答案】(1)y=−x2+2x+3
(2)①53,329;②73或5
【分析】(1)利用待定系数法即可求解;
(2)①作点A关于直线BC的对称点G,连接CG交抛物线于点F,此时,∠BCF=∠BCA,求得G(3,4),利用待定系数法求得直线CF的解析式为:y=13x+3,联立方程组,即可求解;
②分两种情况讨论,由相似三角形的性质和等腰三角形的性质,可求CF的解析式,联立方程可求解.
【详解】(1)解:∵B(3,0)在抛物线y=−x2+bx+3上,
∴y=−32+3b+3,
解得b=2,
∴所求函数关系式为y=−x2+2x+3;
(2)解:①作点A关于直线BC的对称点G,AG交BC于点H,过点H作HI⊥x轴于点I,连接CG交抛物线于点F,此时,∠BCF=∠BCA,如图:
令x=0,y=3;
令y=0,−x2+2x+3=0,
解得:x=3或x=-1,
∵A(-1,0),B(3,0),C(0,3),
∴OB=OC,AB=4,
∴△OCB是等腰直角三角形,则∠OCB=∠OBC=45°,
∴∠HAB=∠OBC=∠AHI=∠BHI=45°,
∴HI= AI=BI=12AB=2,
∴H(1,2),
∴G(3,4),
设直线CG的解析式为:y=kx+3,
把G(3,4)代入得:4=3k+3,
解得:k=13,
∴直线CF的解析式为:y=13x+3,
∴y=−x2+2x+3y=13x+3,解得:x=53y=329,
所以F点的坐标为(53,329);
②当点F在x轴上方时,如图,延长CF交x轴于N,
∵点B(3,0),点C(0,3),
∴OB=OC=3,
∴∠CBO=∠BCO=45°,
∵点A(-1,0),
∴OA=1,∵∠FCE+∠ACO=45°,∠CBO=∠FCE+∠CNO=45°,
∴∠ACO=∠CNO,
又∵∠COA=∠CON=90°,
∴△CAO∽△NCO,
∴COAO=NOCO,
∴31=NO3,
∴ON=9,
∴点N(9,0),
同理可得直线CF解析式为:y=-13x+3,
∴-13x+3=-x2+2x+3,
∴x1=0(舍去),x2=73,
∴点F的横坐标为73;
当点F在x轴下方时,如图,设CF与x轴交于点M,
∵∠FCE+∠ACO=45°,∠OCM+∠FCE=45°,
∴∠ACO=∠OCM,
又∵OC=OC,∠AOC=∠COM,
∴△COM≌△COA(ASA),
∴OA=OM=1,
∴点M(1,0),
同理直线CF解析式为:y=-3x+3,
∴-3x+3=-x2+2x+3,
∴x1=0(舍去),x2=5,
∴点F的横坐标为5,
综上所述:点F的横坐标为5或73.
【点睛】本题是二次函数综合题,考查了二次函数的性质,待定系数法求解析式,相似三角形的判定和性质,全等三角形的判定和性质,两点距离公式,勾股定理等知识,灵活运用这些性质解决问题是本题的关键.
15.(2022·广东深圳·校联考三模)已知抛物线y=ax2+c过点A−2,0和D−1,3两点,交x轴于另一点B.
(1)求抛物线解析式;
(2)如图1,点P是BD上方抛物线上一点,连接AD,BD,PD,当BD平分∠ADP时,求P点坐标;
(3)将抛物线图象绕原点O顺时针旋转90°形成如图2的“心形”图案,其中点M,N分别是旋转前后抛物线的顶点,点E、F是旋转前后抛物线的交点.
①直线EF的解析式是______;
②点G、H是“心形”图案上两点且关于EF对称,则线段GH的最大值是______.
【答案】(1)y=−x2+4
(2)P23,329
(3)①y=x;②1724
【分析】(1)待定系数法求解析式;
(2)过点B作BE⊥x轴交DP延长线与点E,过D作DF⊥x轴交x轴于点F.证明△DAB≌△DEB,求得点E的坐标,进而求得直线DE的解析式为y=13x+103,联立抛物线解析式即可求解;
(3)①根据顺时针旋转90°后点的坐标特征可知对称轴为y=x;
②连接GH,交EF于点M,则GH=2GM,过点G作x轴的垂线,交EF于点N,当GM最大时,△GFE面积最大,设Gm,−m2+4,则Nm,m,根据S△GFE=12GN⋅xE−xF以及二次函数的性质求得当m=−12时,△GFE面积最大,G−12,154,根据①的方法求得H的坐标,根据中点公式求得M的坐标,根据勾股定理求得GH,由GH=2GM即可求解.
(1)
∵y=ax2+c过A−2,0,D−1,3
∴4a+c=0a+c=3 解之得a=−1c=4
∴抛物线解析式为y=−x2+4
(2)
过点B作BE⊥x轴交DP延长线与点E,过D作DF⊥x轴交x轴于点F.
由y=−x2+4,令y=0,得x1=−2,x2=2,则B2,0
∵ yD=xB−xD,即DF=BF,
∴∠DBF=45°,
∴∠DBE=45°
又∵DB=DB,BD平分∠ADP,
∴△DAB≌△DEB,
∴BA=BE,
∵ B2,0
∴E2,4
设直线DE的解析式为y=kx+b,
−k+b=32k+b=4
解得k=13b=103
∴直线DE的解析式为y=13x+103
联立y=−x2+4y=13x+103
解得x=−1y=3,x=23y=329
则P23,329
(3)
①直线EF解析式为y=x.
∵抛物线关于y轴对称,所以旋转后图形关于x轴对称,
∴对于抛物线上任意一点Pa,b关于原点旋转90°后对应点为P1b,−a在旋转后图形上,P1b,−a关于x轴对称的点P2b,a在旋转后图形上,
∵Pa,b与P2b,a关于y=x对称,
∴图形2关于y=x对称,
∴直线EF解析式为y=x
故答案为:y=x
②GH最大值为1724
如图,连接GH,交EF于点M,则GH=2GM,过点G作x轴的垂线,交EF于点N,
∴当GM最大时,△GFE面积最大,
又∵S△GFE=12GN⋅xE−xF
设Gm,−m2+4,则Nm,m
∴GN=yG−yN=−m2+4−m=−m+122+174
∴当m=−12时,△GFE面积最大,G−12,154
由①可知G−12,154关于y=x的对称点H 154,−12
∴ M138,138
∴GM=138+122+154−1382=1728
∴GH的最大值为:GH=2GM=1724
故答案为:1724
【点睛】本题考查了二次函数的性质,旋转的性质,全等三角形的性质与判定,一次函数与二次函数交点问题,掌握以上知识是解题的关键.
16.(2022·山东聊城·统考三模)如如图,在平面直角坐标系中,抛物线y=-12x2+bx+c与x轴交于A(-2,0)、B(4,0)两点(点A在点B的左侧),与y轴交于点C,连接AC、BC,点P为直线BC上方抛物线上一动点,连接OP交BC于点Q.
(1)求抛物线的表达式;
(2)当PQOQ的值最大时,求点P的坐标和PQOQ的最大值;
(3)点M为抛物线上的点,当∠BCM=∠ACO时,求点M的坐标.
【答案】(1)y=−12x2+x+4
(2)PQOQ最大值为12,P2,4
(3)点M的坐标为83,289或8,−20
【分析】(1)运用待定系数法即可求得答案;
(2)运用待定系数法求得直线BC的解析式为y=-x+4,如图1,过点P作PD∥y轴交BC于点D,设P(m,−12m2+m+4),则D(m,-m+4),证明△PDQ∽△OCQ,得出:PQOQ=PDOC=−12m2+2m4=−18(m−2)2+12,运用求二次函数最值方法即可得出答案;
(3)分当点M在x轴下方和当点M在x轴上方两种情况讨论,利用三角函数的定义求解即可.
(1)
解:∵抛物线y=−12x2+bx+c与x轴交于A(-2,0)、B(4,0)两点(点A在点B的左侧),
∴−12×−22−2b+c=0−12×42+4b+c=0,解得:b=1c=4,
∴抛物线的函数表达式为y=−12x2+x+4;
(2)
解:∵抛物线y=−12x2+x+4与y轴交于点C,
∴C0,4,
∴OC=4,
设直线BC的解析式为y=kx+d,把B4,0,C0,4代入,得:
4k+d=0d=4,解得k=−1d=4,
∴直线BC的解析式为y=−x+4,
如图,过点P作PD∥y轴交BC于点D,
设Pm,−12m2+m+4,则Dm,−m+4,
∴PD=−12m2+2m,
∵PD∥OC,
∴△PDQ∽△OCQ,
∴PQOQ=PDOC=−12m2+2m4=−18m−22+12,
∴当m=2时,PQOQ取得最大值12,此时,P2,4;
(3)
解:①如图,当点M在x轴下方时,在x轴上取一点F,使∠BCF=∠ACO,延长CF交抛物线于点M1,过点F作FG⊥BC于点G,过点G作GH⊥AB于点H.
∵点B,C的坐标分别为4,0,0,4,
∴OB=OC,
∴∠CBO=45°,
∴FG=BG,
∵tan∠BCM=tan∠ACO=OAOC=24=12,
∴CG=2FG=2BG.
在Rt△BOC中,BC=2OB=42,设FG=BG=n,
则CG=2n,BC=3n,
∴3n=42,解得n=423,
∴BF=2BG=83,
∴OF=OB−BF=43,
∴点F的坐标为43,0.
设直线CF的表达式为y=k1x+b1,
∴43k1+b1=0b1=4,
∴k1=−3b1=4,
∴直线CF的表达式为y=−3x+4,
∴y=−12x2+x+4y=−3x+4,
解得x1=0y1=4(舍去),x2=8y2=−20,
∴点M的坐标为8,−20.
②如图,当点M在x轴上方时,过点B作BH⊥BC,交CM2于点H,过点H作HN⊥x轴于点N,
∴∠CBH=90°.
∵OB=OC,
∴∠CBO=45°,
∴∠BHN=∠HBN=45°,
∴BN=HN.
∵∠BCM=∠ACO,
∴tan∠BCM=tan∠ACO=BHBC=OAOC=24=12,
∴BH=12BC=22,
∴HN=BN=2
∴ON=OB+BN=6,
∴点H的坐标为6,2.
设直线CH的表达式为y=px+q,
∴6p+q=2q=4,解得p=−13q=4,
∴直线CH的表达式为y=−13x+4,
∴y=−12x2+x+4y=−13x+4
解得x1=0y1=4(舍去),x2=83y2=289,
∴点M的坐标为83,289.
综上可知,点M的坐标为83,289或8,−20.
【点睛】本题是二次函数综合题,考查了待定系数法,二次函数的图象和性质,解直角三角形,相似三角形的判定和性质,熟练运用数形结合思想、分类讨论思想是解题关键.
17.(2022·辽宁沈阳·统考二模)如图,在平面直角坐标系中,抛物线y=ax2+bx+4a≠0经过点A3,4和点B−1,0,连接AB,过点A作AD⊥x轴于点D,点P在直线AB上方的抛物线上,过点P作PE∥AD交x轴于点E,交线段AB于点G,连接PD交线段AB于点Q.
(1)求抛物线的表达式;
(2)当GQ=AQ时,设点P的横坐标为m,求m的值;
(3)在(2)的条件下,线段BE上有一点F,直线AD上有一点K,连接KF、GF,当∠FKD=2∠FGB,且KF=8时,直接写出点K的纵坐标.
【答案】(1)y=−x2+3x+4
(2)m=1
(3)2+27或−2−27
【分析】(1)直接利用待定系数法求解即可;
(2)先求出直线AB的解析式为y=x+1,然后证明△PGQ≌△DAQ得到PG=AD=4,再由点P的坐标为m,−m2+3m+4,点G的坐标为(m,m+1),得到PG=−m2+3m+4−m−1=4,由此求解即可;
(3)如图所示,过点F作FH⊥AB于H,过点K作KQ平分∠FKD交x轴于Q,过点Q作QM⊥KF于M,连接FG,设BF=2t,QD=s,KD=k,则DF=4−2t,先证明∠HBF=∠HFB=45°,得到HB=HF=2t,再由(2)得m=1,求得BG=22,则HG=22−2t,tan∠FGH=HFHG=t2−t;根据角平分线的定义和性质得到QM=QD=s,∠FGH=∠QKD,再由S△FKD=S△FQK+S△DQK=12DF⋅DK=12KF⋅QM+12DQ⋅DK,推出s=k4−2t8+k,则tan∠QKQ=tan∠FGH=sk=t2−t,可以推出k=22−t2−8tt=2t2−16t+8t,
在Rt△FKD中,DF2+DK2=KF2=64,得到4−2t2+2t2−16t+8t2=64,由此即可求出t的值即可得到答案.
(1)
解:∵抛物线y=ax2+bx+4a≠0经过点A3,4和点B−1,0,
∴9a+3b+4=4a−b+4=0,
∴a=−1b=3,
∴抛物线解析式为y=−x2+3x+4;
(2)
解:设直线AB的解析式为y=kx+b1,
∴−k+b1=03k+b1=4,
∴k=1b=1,
∴直线AB的解析式为y=x+1,
∵PE∥AD,
∴∠PGQ=∠DAQ,∠GPQ=∠ADQ,
又∵AQ=GQ,
∴△PGQ≌△DAQ(AAS),
∴PG=AD=4,
∵点P的横坐标为m,
∴点P的坐标为m,−m2+3m+4,点G的坐标为(m,m+1),
∴PG=−m2+3m+4−m−1=4,
∴m2−2m+1=0,
解得m=1;
(3)
解:如图所示,过点F作FH⊥AB于H,过点K作KQ平分∠FKD交x轴于Q,过点Q作QM⊥KF于M,连接FG,设BF=2t,QD=s,KD=k,则DF=4−2t,
∵点B的坐标为(-1,0),点A的坐标为(3,4),
∴BD=AD=4,
∴∠ABD=45°,
∵FH⊥AB,
∴∠HBF=∠HFB=45°,
∴HB=HF=2t,
由(2)得m=1,
∴点G的坐标为(1,2),
∴BE=GE=2,
∴BG=BE2+GE2=22,
∴HG=BG−HB=22−2t,
∴tan∠FGH=HFHG=t2−t;
∵KQ平分∠FKD,QM⊥FK,QD⊥DK,∠FKD=2∠FGB,
∴QM=QD=s,∠FGH=∠QKD,
∴S△FKD=S△FQK+S△DQK=12DF⋅DK=12KF⋅QM+12DQ⋅DK,
∴12k4−2t=12×8s+12sk,
∴s=k4−2t8+k,
∴tan∠QKQ=tan∠FGH=sk=t2−t,
∴4−2t8+k=t2−t,
∴k=22−t2−8tt=2t2−16t+8t,
在Rt△FKD中,DF2+DK2=KF2=64,
∴4−2t2+2t2−16t+8t2=64,
∴16−16t+4t2+4t4−64t3+288t2−256t+64t2=64,
∴16t2−16t3+4t4+4t4−64t3+288t2−256t+64=64t2,
∴8t4−80t3+240t2−256t+64=0,
∴t4−10t3+24t2−32t+8=0,
∴t2t2−10t+16+14t2−32t+8=0,
∴t2t−2t−8+27t−2t−2=0,
∴t3−8t2+14t−4t−2=0,
∴tt2−8t+12+2t−2t−2=0,
∴tt−2t−6+2t−2t−2=0,
∴t2−6t+2t−22=0,
∵点F在BE上,
∴BF=2t≤BE=2,
∴t≤1,
∴t2−6t+2=0,
解得t=3−7或t=3+7(舍去),
∴k=2t2−16t+8t=2t2−6t+2−4t+4t=4−4tt=4−12+473−7=27+2,
∴DK=27+2,
∴点K的纵坐标为2+27或−2−27.
【点睛】本题主要考查了二次函数综合,一次函数与几何综合,勾股定理,解直角三角形,角平分线的性质,等腰直角三角形的性质与判定,全等三角形的性质与判定等等,熟练掌握二次函数的相关知识是解题的关键.
18.(2022·山东济南·统考一模)如图,抛物线y=ax2+2x−3与x轴交于A、B两点,且B(1,0).
(1)求抛物线的解析式和点A的坐标;
(2)如图1,点P是直线y=x上在x轴上方的动点,当直线y=x平分∠APB时,求点P的坐标;
(3)如图2,已知直线y=23x−49分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
【答案】(1)抛物线解析式为y=x2+2x-3,A点坐标为(-3,0);
(2)P点坐标为(32,32);
(3)以QD为腰的等腰三角形的面积最大值为5413.
【分析】(1)把B点坐标代入抛物线解析式可求得a的值,可求得抛物线解析式,再令y=0,可解得相应方程的根,可求得A点坐标;
(2)当点P在x轴上方时,连接AP交y轴于点B′,可证△OBP≌△OB′P,可求得B′坐标,利用待定系数法可求得直线AP的解析式,联立直线y=x,可求得P点坐标;
(3)过Q作QH⊥DE于点H,由直线CF的解析式可求得点C、F的坐标,结合条件可求得tan∠QDH,可分别用DQ表示出QH和DH的长,分DQ=DE和DQ=QE两种情况,分别用DQ的长表示出△QDE的面积,再设出点Q的坐标,利用二次函数的性质可求得△QDE的面积的最大值.
(1)
解:把B(1,0)代入y=ax2+2x-3,
可得a+2-3=0,解得a=1,
∴抛物线解析式为y=x2+2x-3,
令y=0,可得x2+2x-3=0,解得x=1或x=-3,
∴A点坐标为(-3,0);
(2)
解:若y=x平分∠APB,则∠APO=∠BPO,
如图1,若P点在x轴上方,PA与y轴交于点B′,
由于点P在直线y=x上,可知∠POB=∠POB′=45°,
在△BPO和△B′PO中
{∠POB=∠POB′OP=OP∠BPO=∠B′PO,
∴△BPO≌△B′PO(ASA),
∴BO=B′O=1,
设直线AP解析式为y=kx+b,把A、B′两点坐标代入可得
{−3k+b=0b=1,解得{k=13b=1,
∴直线AP解析式为y=13x+1,
联立{y=xy=13x+1,解得{x=32y=32,
∴P点坐标为(32,32);
(3)
解:如图2,作QH⊥CF,交CF于点H,设抛物线交y轴于点M.
∵CF为y=23x−49,
∴可求得C(23,0),F(0,-49),
∴tan∠OFC=OCOF=32,
∵DQ∥y轴,
∴∠QDH=∠MFD=∠OFC,
∴tan∠HDQ=32,
不妨设DQ=t,DH=213t,HQ=313t,
∵△QDE是以DQ为腰的等腰三角形,
∴若DQ=DE,则S△DEQ=12DE•HQ=12×313t×t=31326t2,
若DQ=QE,则S△DEQ=12DE•HQ=12×2DH•HQ=12×413t×313t=613t2,
∵31326t2<613t2,
∴当DQ=QE时△DEQ的面积比DQ=DE时大.
设Q点坐标为(x,x2+2x-3),则D(x,23x−49),
∵Q点在直线CF的下方,
∴DQ=t=23x−49-(x2+2x-3)=-x2-43x+239=-(x+23)2+3,
当x=-23时,tmax=3,
∴(S△DEQ)max=613t2=5413,
即以QD为腰的等腰三角形的面积最大值为5413.
【点睛】本题主要考查二次函数的综合应用,涉及知识点有待定系数法、角平分线的定义、全等三角形的判定和性质、三角形的面积、等腰三角形的性质、二次函数的性质及分类讨论等.在(2)中确定出直线AP的解析式是解题的关键,在(3)中利用DQ表示出△QDE的面积是解题的关键.本题考查知识点较多,综合性较强,计算量大,难度较大.
19.(2020·江苏常州·统考二模)如图,顶点坐标为(3,4)的抛物线y=ax2+bx+c交x轴于A,B两点,交y轴于点C(0,−5).
(1)求a,b的值;
(2)已知点M在射线CB上,直线AM与抛物线y=ax2+bx+c的另一公共点是点P.
①抛物线上是否存在点P,满足AM:MP=2:1,如果存在,求出点P的横坐标;如果不存在,请说明理由;
②连接AC,当直线AM与直线BC的夹角等于∠ACB的2倍时,请直接写出点M的坐标.
【答案】(1)-1;6
(2)①存在,5+172或5+332或5−332;②(136,−176);(236,−76)
【分析】(1)由题意知,9a+3b+c=4−b2a=3c=−5,求出a,b,c的值即可;
(2)①由(1)可知,抛物线的解析式为y=−x2+6x−5,A1,0,B5,0,设直线BC的函数解析式为y=kx+b,待定系数法求得直线BC的函数解析式为y=x−5,设Pm,−m2+6m−5,如图1,当1
(1)
解:由题意知,9a+3b+c=4−b2a=3c=−5,
解得a=−1b=6c=−5,
∴a=−1,b=6.
(2)
解:由(1)可知,抛物线的解析式为y=−x2+6x−5,
令−x2+6x−5=0,
则x−1x−5=0,
解得x=1或x=5,
∴A1,0,B5,0,
设直线BC的函数解析式为y=kx+b,
将B,C代入得5k+b=0b=−5,
解得k=1b=−5,
∴直线BC的函数解析式为y=x−5,
设Pm,−m2+6m−5,如图1,
当1
解得m=5+172,m=5−172(不合题意,舍去),
∴m=5+172时,AM:MP=2:1;
当m>5时,AM2:M2P2=2:1,则M21+23(m−1),23−m2+6m−5,
∴1+23(m−1)−5=23−m2+6m−5,
解得m=5+332,m=5−332(不合题意,舍去)
∴当m=5+332时,AM:MP=2:1;
当m<0时,AM3:M3P3=2:1,则M31−23(1−m),23−m2+6m−5,
∴1−23(1−m)−5=23−m2+6m−5,
解得m=5−332,m=5+332(不合题意,舍去)
∴当m=5−332时,AM:MP=2:1;
综上所述,存在点P,满足AM:MP=2:1,点P的横坐标为5+172或 5+332或5−332.
②解:如图2,作AN⊥BC于N,NH⊥x轴于H,作AC的垂直平分线交BC于M1,交AC于E,交y轴于F,连接AF,作M1关于AN的对称点M2,
由题意知,AF=CF,设OF=x,则AF=CF=5−x,
在Rt△AOF中,由勾股定理得AF2−OF2=OA2,即5−x2−x2=1,
解得x=125,
∴F0,−125,
设直线EF的解析式为y=px+q,将E,F点坐标代入得−12p+q=−52q=−125,
解得p=−15q=−125,
∴直线EF的解析式为y=−15x−125,
联立得y=−15x−125y=x−5,
解得x=136y=−176,
∴M136,−176
由对称的性质可知,∠AM2C=∠AM1B,∠AM2C=2∠ACB,M1N=M2N,
∵OB=OC,
∴∠ABC=45°,
∵∠ANB=90°,∠BAN=45°,
∴AN=BN,
∴HN=12AB=2,
∴N3,−2,
∴M2236,−76,
∴点M的坐标为136,−176,236,−76.
【点睛】本题考查了二次函数解析式,二次函数图象,二次函数与线段、角度综合,垂直平分线的性质,对称的性质,勾股定理,等腰三角形的判定与性质等知识.解题的关键在于对知识的熟练掌握与灵活运用.
20.(2022·山东济南·统考二模)如图,抛物线y=x2+bx+c与x轴分别交于A,B两点(点A在点B的左侧),与y轴交于点C,若A−1,0且OC=3OA.
(1)求该抛物线的函数表达式;
(2)如图1,点D是该抛物线的顶点,点Pm,n是第二象限内抛物线上的一个点,分别连接BD、BC、BP,当∠PBA=2∠CBD时,求m的值;
(3)如图2,∠BAC的角平分线交y轴于点M,过M点的直线l与射线AB,AC分别交于E,F,已知当直线l绕点M旋转时,1AE+1AF为定值,请直接写出该定值.
【答案】(1)y=x2-2x−3
(2)−74
(3)10+1010
【分析】(1)求出A、C坐标,代入解析式计算即可;
(2)取BC中点G,作GH⊥BC于H,连接CH,过C作CM⊥BD于M,过P作PN⊥x轴于N,由抛物线顶点D坐标为(1,-4),B(3,0),C(0,-3),可得∠BCD=90°,GH∥CD,从而H为BD中点,CH=BH= 12BD= 5,由面积法得CM=BC⋅CDBD=355,故tan∠CHM= tan∠PBA=34,设P(m,m2-2m-3),表示出tan∠PBA列方程计算即可;
(3)过M作MG∥x轴交AC于G,过F作FT∥x轴交AM于T,过C作CQ∥x轴交AM于Q,由MG∥FT∥CQ∥OA,得△COA∽△CMG,△ACQ∽AGM,证明1AE+1AF=1GM=1OA+1AC即可.
(1)
∵A−1,0,
∴OA=1,
∵OC=3OA,
∴OC=3,
∴C(0,−3)
将A(−1,0),C(0,−3),代入y=x2+bx+c得:0=1−b+cc=−3,
解得:b=−2c=−3,
∴该抛物线的解析式为y=x2-2x−3;
(2)
取BC中点G,作GH⊥BC于H,连接CH,过C作CM⊥BD于M,过P作PN⊥x于轴N,如图:
由y=x2−2x−3得抛物线顶点D坐标为1,−4,而B(3,0),C(0,−3),
∴BC=32,CD=2,BD=25,
∴BC2+CD2=20,BD2=20,
∴BC2+CD2=BD2,
∴∠BCD=90°,
∵GH⊥BC,
∴GH∥CD,
∵G为BC中点,
∴H为BD中点,
∴CH=BH=12BD=5,
∴∠CHM=2∠CBD=∠PBA,
∵CM=BC⋅CDBD=355,
∴MH=CH2−CM2=455,
∴tan∠CHM=34,
∴tan∠PBA=34,即PNBN=34,
设Pm,m2−2m−3,
则m2−2m−33−m=34
解得m1=3(与B重合,舍去)或m2=−74,
∴m的值为−74;
(3)
过M作MG∥x轴交AC于G,过F作FT∥x轴交AM于T,过C作CQ∥x轴交AM于Q.如图:
∵MG∥x轴,FT∥x轴,CD∥x轴,
∴MG∥FT∥CQ∥OA,
∴△COA∽△CMG,△ACQ∽△AGM,
∴GMOA=CGAC,GMCQ=AGAC,
∴GMOA+GMCQ=CGAC+AGAC=1
∴1OA+1CQ=1GM,
∵AM平分∠BAC,
∴∠CAM=∠BAM=∠AQC,
∴AC=CQ,
∴1OA+1AC=1GM,
同理可得1AE+1AF=1GM,
由(1)可知:A−1,0,C0,−3,
∴AC=10,
∴1AE+1AF=1GM=1OA+1AC=11+110=10+1010
【点睛】本题考查二次函数综合应用,涉及待定系数法、二次函数图象上点坐标特征、锐角三角函数、相似三角形的判定与性质等知识,解题的关键是作辅助线,构造相似三角形解决问题.
21.(2022·江苏淮安·统考一模)如图,已知A(−2,0),B(3,0),抛物线y=ax2+bx+4经过A、B两点,交y轴于点C.点P是第一象限内抛物线上的一点,点P的横坐标为m.过点P作PM⊥x轴,垂足为点M,PM交BC于点Q.过点P作PN⊥BC,垂足为点N.
(1)求抛物线的函数表达式;
(2)请用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,最大值是多少?
(3)连接PC,在第一象限的抛物线上是否存在点P,使得∠BCO+2∠PCN=90°?若存在,请直接写出m的值;若不存在,请说明理由.
【答案】(1)y=−23x2+23x+4
(2)PN=−25m2+65m,当m=32时,有最大值910
(3)存在,m=74
【分析】(1)直接利用待定系数法求解即可;
(2)先求出点C的坐标,从而求出直线BC的解析式,则点P的坐标为m,−23m2+23m+4,点Q的坐标为m,−43m+4,PQ=−23m2+2m,再利用勾股定理求出BC=5,得到sin∠BOC=OBBC=35,再证明∠PQN=∠BCO,得到sin∠PQN=PNPQ=35,则PN=35PQ=−25m2+65m=−25m+322+910,由此求解即可;
(3)如图所示,过点C作CD⊥PM于D,则四边形OCDM是矩形 ,可以得到∠OCD=90°,点D的纵坐标为4,可以证明∠PCD=∠PCN,得到PD=PN=−25m2+65m,则4−−23m2+23m+4=−25m2+65m,由此即可得到答案.
(1)
解:∵A(−2,0),B(3,0),抛物线y=ax2+bx+4经过A、B两点,
∴4a−2b+4=09a−3b+4=0,
∴a=−23b=23,
∴抛物线解析式为y=−23x2+23x+4;
(2)
解:设直线BC的解析式为y=kx+b1,
∵点C是抛物线y=−23x2+23x+4与y轴的交点,
∴点C的坐标为(0,4),
∴3k+b1=0b1=4,
∴k=−43b1=4,
∴直线BC的解析式为y=−43x+4,
∴点P的坐标为m,−23m2+23m+4,点Q的坐标为m,−43m+4,
∴PQ=−23m2+23m+4+43m−4=−23m2+2m,
∵OC=4,OB=3,
∴BC=OC2+OB2=5,
∴sin∠BCO=OBBC=35,
∵PM⊥x轴,
∴PM∥OC,
∴∠PQN=∠BCO,
又∵PN⊥BC,
∴sin∠PQN=PNPQ=35,
∴PN=35PQ=−25m2+65m=−25m+322+910,
∴当m=32时,PN有最大值910;
(3)
解:存在,m的值为74;
理由:如图所示,过点C作CD⊥PM于D,则四边形OCDM是矩形,
∴∠OCD=90°,点D的纵坐标为4,
∴∠OCB+∠BCD=90°,
∵∠OCB+2∠PCN=90°,
∴∠BCD=2∠PCN,
∴∠PCD=∠PCN,
∴PD=PN=−25m2+65m,
∴4−−23m2+23m+4=−25m2+65m,
∴4m2−7m=0,
解得m=74或m=0(舍去);
因此存在,m的值为74.
【点睛】本题主要考查了二次函数综合,一次函数与几何综合,角平分线的性质,解直角三角形,待定系数法求函数解析式,勾股定理等等,熟知二次函数的相关知识是解题的关键.
22.(2022·辽宁沈阳·沈阳市南昌初级中学(沈阳市第二十三中学)校考一模)如图,抛物线y=ax2+bx+2与x轴相交于A、B两点,与y轴相交于点C,已知B点的坐标为4,0,抛物线的对称轴为直线x=32,点D是BC上方抛物线上的一个动点.
(1)求抛物线的函数表达式;
(2)当△BCD的面积为74时,求点D的坐标;
(3)过点D作DE⊥BC,垂足为点E,是否存在点D,使得△CDE中的某个角等于∠ABC的2倍?若存在,请直接写出点D的横坐标;若不存在,请说明理由.
【答案】(1)y=−12x2+32x+2.
(2)D72,98或12,218.
(3)点D的横坐标为2或2911.
【分析】(1)利用待定系数法列方程组求解抛物线的解析式即可;
(2)如图,连接OD,设Dx,−12x2+32x+2,0
∴16a+4b+2=0−b2a=32,
解得:a=−12b=32, 经检验符合题意,
所以抛物线的解析式为:y=−12x2+32x+2.
(2)解:如图,连接OD,设Dx,−12x2+32x+2,0
∴S△BOC=12×4×2=4, S△DOC=12×2x=x,
S△DOB=12×4×−12x2+32x+2=−x2+3x+4,
∴S△BCD=−x2+3x+4+x−4=−x2+4x=74,
解得:x1=72,x2=12,
∴D72,98或12,218.
(3)解:如图,过D作DQ∥y轴交BC于Q, 过C作CF⊥DQ于F, 点D作DE⊥BC,垂足为点E,则CF∥x轴,
∴∠FCB=∠ABC,
当∠DCE=2∠ABC时,
∴∠DCF=∠BCF,∠CDF=∠CQF,
∴CD=CQ,DF=FQ,
设BC的解析式为:y=mx+n, 由C0,2,B4,0可得:
4m+n=0n=2, 解得m=−12n=2,
所以BC为:y=−12x+2,
设Dx,−12x2+32x+2,0
∴−12x2+32x+2−2=2−−12x+2,
解得:x1=2,x2=0, (x=0不符合题意,舍去)
∴D2,3,
当∠CDE=2∠ABC时,作C关于OB的对称点F,过点C作CN⊥BF于点N,交OB于H.作点N关于BC的对称点P,连接NP交BC于点Q,如图所示.
∴F0,−2,BC=BF=22+42=25,
∴12×4×4=12×25×CN,
∴CN=855,
∴BN=252−8552=655,
∵ 点N关于BC的对称点为点P,
∴CP=CN=855,BN=BP=655,
设Px,y,
∴x2+y−22=8552x−42+y2=6552,
整理得:y=2x−225,
∴125x2−640x+704=0, 即25x−885x−8=0,
解得:x1=8825,x2=85,
∴x=8825y=6625或x=85y=−65,
∵∠CHA=∠NHB,
∴∠OCH=∠OBF,
∴tan∠OCH=tan∠OBF=12,
∴OH2=12, 即OH=1,H1,0, 而C0,2,
则CH的解析式为:y=−2x+2,
∵y=2x−225y=−2x+2
解得:x=85y=−65,
所以P8825,6625,
∵点C(0,2),P8825,6625,
同理可得直线CP的解析式为y=211x+2.
将y=211x+2代入y=−12x2+32x+2,
整理,得:11x2−29x=0,
解得:x1=0(舍去),x2=2911,
∴点D的横坐标为2911.
综上所述:存在点D,使得△CDE的某个角恰好等于∠ABC的2倍,点D的横坐标为2或2911.
【点睛】本题是二次函数综合题,考查了勾股定理、等腰三角形的性质、平行线的判定与性质、待定系数法求函数的表达式等知识,解题的关键是根据题意综合运用以上知识点,注意分类讨论思想的运用.
23.(2022·云南昆明·校联考模拟预测)在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c交x轴于A−1,0,B4,0两点,与y轴交于点C0,3.
(1)求抛物线的函数解析式;
(2)如图1,点D为直线BC上方抛物线上一动点,连接AD,交BC于点E,求DEAE的最大值;
(3)如图2,点P为抛物线上一动点,是否存在点P,使得2∠PCB=∠OCB,若存在,请直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)y=−34x2+94x+3
(2)DEAE的最大值为45
(3)存在,P173,−253或10733,875363
【分析】(1)直接根据两点式写出抛物线的表达式y=ax+1x−4a≠0,然后代入点C0,3求出a即可.
(2)如图1,过点D作DF∥x轴交BC于点F,根据ΔEDF∼ΔEAB得出DEAE=DFAB,从而将求DEAE的最大值转换为求DFAB的最大值,由于AB=5,故只需求出DF最大值即可得出答案.
(3)由2∠PCB=∠OCB,作∠OCB的角平分线,此时点P在角平分线上或者在角平分线关于CB的对称直线上,分别求出两条直线解析式,然后联立抛物线即可求出点P的坐标.
(1)
设y=ax+1x−4a≠0,
将C0,3代入上式,得−4a=3,解得a=−34,
∴y=−34x+1x−4,即y=−34x2+94x+3.
(2)
如图1,过点D作DF∥x轴交BC于点F,
∵DF∥AB,
∴△EDF∽△EAB,
∴DEAE=DFAB,
设直线BC的解析式为y=kx+bk≠0,
将B4,0和C0,3分别代入上式,得4k+b=0b=3,
解得k=−34b=3,
∴直线BC的解析式为y=−34x+3,
∵点D为直线BC上方抛物线上一动点,
∴设Dm,−34m2+94m+30
∴Fm2−3m,−34m2+94m+3,
∴DF=−m2+4m,
∵a=−1<0,
∴开口向下,
当m=−b2a=−42×−1=2时,DF最大=4,
∵A−1,0,B4,0,
∴AB=5,
∴DEAE的最大值为45.
(3)
答:存在,P173,−253或10733,875363.
①如图2,作∠OCB的角平分线交x轴于点M,交抛物线于点P1,过点M作MN⊥BC于点N.
∵CP1是∠OCB的角平分线,MN⊥BC,MO⊥OC,
∴MO=MN,
在Rt△OCM和Rt△NCM中CM=CMOM=NM,
∴Rt△OCM≌Rt△NCM(HL),
∴CN=CO=3,
在Rt△OCB中,CB=OC2+OB2=5,
∴BN=CB-CN=5-3=2,
设OM=MN=x,则BM=4-x,
在Rt△MNB中,∵MN2+NB2=MB2,
∴x2+22=(4−x)2 ,解得x=32,
∴M32,0;
设直线CM的解析式为y=k1x+b1k1≠0,
将C0,3和M32,0分别代入上式得b1=332k1+b1=0,
解得k1=−2b1=3,
∴直线CM的解析式为y=-2x+3,
联立y=−34x2+94x+3y=−2x+3得x1=0(舍),x2=173,
将x=173代入y=-2x+3中得:y=−253,
∴P1173,−253.
②如图3,延长MN至Q,使得MN=NQ,连接CQ交抛物线于P2,过N作NR⊥AB于R.
在ΔCNM和ΔCNQ中CN=CN∠CNM=∠CNQMN=NQ,
∴ΔCNM ≅ ΔCNQ(SAS),
∴∠BCP2=∠MCB,即2∠BCP2=∠OCB,
∵S△MNB=12MN⋅NB=12MB⋅NR,
∴NR=MN⋅NRMB=32×252=65,
∴MR=MN2−NR2=322−652=910,
∴N125,65.根据中点坐标公式得Q3310,125;
设直线CQ的解析式为y=k2x+b2k2≠0,
将C0,3和Q3310,125分别代入上式得b2=33310k2+b2=125,
解得k2=−211b2=3,
∴直线CQ的解析式为y=−211x+3,
联立y=−34x2+94x+3y=−211x+3得x1=0(舍),x2=10733,
将x=10733代入y=−211x+3中得y=875363,
∴P210733,875363.
综上所述,存在满足条件的点P173,−253或10733,875363.
【点睛】本题属于二次函数与几何综合题,涉及相似三角形的判定与性质,全等三角形的判定与性质,角平分线的性质等知识,综合性较强,解题的关键是读懂题意,巧妙转化,将复杂的几何问题转化为代数问题.
24.(2022·山东济南·统考二模)抛物线y=ax2+bx+c的顶点坐标为(1,4),与x轴交于点A,B(3,0)两点,与y轴交于点C,点M是抛物线上的动点.
(1)求这条抛物线的函数表达式;
(2)如图1,若点M在直线BC上方抛物线上,连接AM交BC于点E,求MEAE的最大值及此时点M的坐标;
(3)如图2,已知点Q(0,1),是否存在点M,使得tan∠MBQ=12?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)y=−x2+2x+3;
(2)916;(32,154);
(3)存在;(−87,−2949)或(0,3)
【分析】(1)因为已知抛物线的顶点坐标,所以将抛物线设为顶点式,将B坐标代入求解即可;
(2)过点M作MM1⊥x轴交直线BC于点M1,过点A作AA1⊥x轴交直线BC于点A1,先证△MM1E∽△AA1E得到对应边的比值相等,设M(m,−m2+2m+3),通过相似三角形的性质得到MEAE间的比,然后根据抛物线的性质即可求出最值,进而求得M坐标;
(3)取线段BQ的中点G,再将QG绕点Q旋转90°得到QG′,则tan∠MBQ=12,直线BG′与抛物线的交点即为点M,然后分类讨论,分为将QG绕点Q顺时针旋转90°,将QG绕点Q逆时针旋转90°,通过联立方程组的方法即可求得M的坐标.
(1)
解:∵抛物线过顶点(1,4),
所以可以设抛物线解析式为:y=a(x−1)2+4,
将B(3,0)代入得,a=−1,
∴抛物线的解析式为:y=−(x−1)2+4,
即:y=−x2+2x+3;
(2)
如图,过点M作MM1⊥x轴交直线BC于点M1,过点A作AA1⊥x轴交直线BC于点A1,
∵直线BC过点C(0,3) ,
∴设直线BC的表达式为:y=kx+3,
将B(3,0)代入,
得k=-1,
∴lBC:y=−x+3,
∵MM1∥AA1,
∴∠AA1E=∠MM1E,∠A1AE=∠M1ME,
∴△MM1E∽△AA1E,
∴MEAE=MM1AA1,
设M(m,−m2+2m+3),则M1(m,−m+3),
∴MM1=−m2+2m+3-(−m+3)=−m2+3m,
令−x2+2x+3=0,解得x1=−1,x2=3,
∴A(-1,0),
∵lBC:y=−x+3, 令x=−1,解得y=4,
∴A1(-1,4),
∴AA1=4,
∴MEAE=MM1AA1=−m2+3m4=−14m2+34m,
∵−14<0,
当m=−b2a=−342×(−14)=32时,MEAE最大,
把m=32代入得,MEAE=−94+924=916,
把m=32代入M(m,−m2+2m+3),
解得M点坐标为(32,154);
(3)
取线段BQ的中点G,再将QG绕点Q旋转90°得到QG′,
则tan∠MBQ=12,直线BG′与抛物线的交点即为点M,
①将QG绕点Q顺时针旋转90°,得到QG′,
分别过点G′、点B作x轴垂线,与过Q点的水平线分别交于点N、Z,
∵QG绕点Q旋转90°得到QG′,
∴∠BOG′=90°,
∵NZ∥x轴,
∴∠N=∠Z=90°,
∵∠NQG′+NG′Q=90°,∠NQG′+∠BQZ=90°,
∴NG′Q=BQZ,
∴△NQG′∽△ZBQ,
∵G是QB的中点,QG=QG′,
∴QG′QB=QGQB=12,
∴NG′=12QZ=32,QN=12BZ=12,
∴xG′=−QN=−12,yG′=−(NG′−OQ)=−(32−1)=−12,
∴G′(−12,−12),
设lBG′:y=kx+b,将B(3,0),G′(−12,−12)代入,
得{3k+b=0−12k+b=−12,解得{k=17b=−37,
∴lBG′:y=17x−37,
由{y=17x−37y=−x2+2x+3,
解得:{x=−87y=−2949或{x=3y=0(舍去),
∴M(−87,−2949);
②如图,将线段QG绕点Q逆时针旋转90°得到QG″,
连接G″B并延长交抛物线于点M,过G″作x轴平行线交y轴于点L,
∵旋转90°,∴∠BQG″=90°,
∵∠LQG″+∠LG″Q=90°,∠LQG″+∠OQB=90°,
∴∠LG″Q=∠OQB,
又∵∠BOQ=∠QLG″=90°,
∴△LQG″∽△OBQ,且相似比为QG″QB=12,
∴LG″=12OQ=12,LQ=12OB=32,
∴xG″=LG″=12,yG″=OQ+LQ=1+32=52,
∴G″(12,52),
又∵B(3,0),
设lBG″:y=kx+b,
将G″(12,52),B(3,0)代入,
得{12k+b=523k+b=0,解得{k=−1b=3,
∴lBG″:y=−x+3,
由{y=−x+3y=−x2+2x+3 ,
解得:{x=0y=3或{x=3y=0(舍去),
∴M(0,3),
综上所述,点M的坐标为(−87,−2949)或(0,3).
【点睛】本题是一道二次函数综合题,主要考查了相似三角形的判定与性质,角的存在性问题等,解决问题的关键是做横平竖直线,将“斜线段”转化为“垂线段”,利用函数思想解决最题.
专题26二次函数与线段周长压轴问题-中考数学压轴大题之经典模型培优案(全国通用): 这是一份专题26二次函数与线段周长压轴问题-中考数学压轴大题之经典模型培优案(全国通用),文件包含专题26二次函数与线段周长压轴问题-中考数学压轴大题之经典模型培优案解析版docx、专题26二次函数与线段周长压轴问题-中考数学压轴大题之经典模型培优案原卷版docx等2份试卷配套教学资源,其中试卷共91页, 欢迎下载使用。
专题31二次函数与圆压轴问题-中考数学压轴大题之经典模型培优案(全国通用): 这是一份专题31二次函数与圆压轴问题-中考数学压轴大题之经典模型培优案(全国通用),文件包含专题31二次函数与圆压轴问题-中考数学压轴大题之经典模型培优案解析版docx、专题31二次函数与圆压轴问题-中考数学压轴大题之经典模型培优案原卷版docx等2份试卷配套教学资源,其中试卷共94页, 欢迎下载使用。
专题30二次函数与动点压轴问题-中考数学压轴大题之经典模型培优案(全国通用): 这是一份专题30二次函数与动点压轴问题-中考数学压轴大题之经典模型培优案(全国通用),文件包含专题30二次函数与动点压轴问题-中考数学压轴大题之经典模型培优案解析版docx、专题30二次函数与动点压轴问题-中考数学压轴大题之经典模型培优案原卷版docx等2份试卷配套教学资源,其中试卷共96页, 欢迎下载使用。