高中数学5.4 三角函数的图象与性质优质第2课时2课时导学案

这是一份高中数学5.4 三角函数的图象与性质优质第2课时2课时导学案，共13页。

学习目标 1.掌握y＝sin x，y＝cs x的最大值与最小值，并会求简单三角函数的值域和最值.2.掌握y＝sin x，y＝cs x的单调性，并能利用单调性比较大小.3.会求函数y＝Asin(ωx＋φ)及y＝Acs(ωx＋φ)的单调区间．








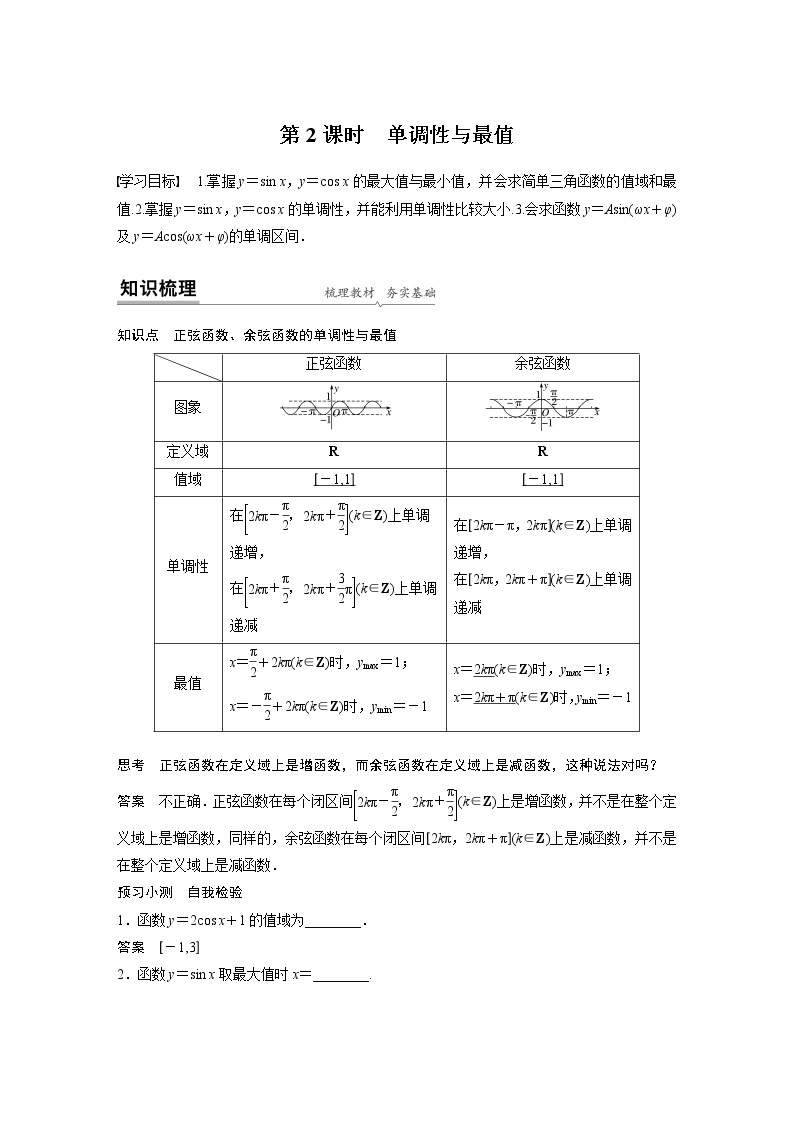
知识点 正弦函数、余弦函数的单调性与最值





思考 正弦函数在定义域上是增函数，而余弦函数在定义域上是减函数，这种说法对吗？


答案 不正确．正弦函数在每个闭区间eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ－\f(π,2)，2kπ＋\f(π,2)))(k∈Z)上是增函数，并不是在整个定义域上是增函数，同样的，余弦函数在每个闭区间[2kπ，2kπ＋π](k∈Z)上是减函数，并不是在整个定义域上是减函数．


预习小测 自我检验


1．函数y＝2cs x＋1的值域为________．


答案 [－1,3]


2．函数y＝sin x取最大值时x＝________.


答案 eq \f(π,2)＋2kπ，k∈Z


3．函数y＝sin xeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)≤x≤π))的值域为________．


答案 [0,1]


4．函数y＝－cs x的单调递减区间是________；单调递增区间是________．


答案 [－π＋2kπ，2kπ](k∈Z) [2kπ，2kπ＋π](k∈Z)





一、求正弦、余弦函数的单调区间


例1 求函数y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3)))的单调区间．


解 令z＝x－eq \f(π,3)，则y＝2sin z.


∵z＝x－eq \f(π,3)是增函数，


∴y＝2sin z单调递增(减)时，


函数y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3)))也单调递增(减)．


由z∈eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ－\f(π,2)，2kπ＋\f(π,2)))(k∈Z)，


得x－eq \f(π,3)∈eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ－\f(π,2)，2kπ＋\f(π,2)))(k∈Z)，


即x∈eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ－\f(π,6)，2kπ＋\f(5π,6)))(k∈Z)，


故函数y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3)))的单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ－\f(π,6)，2kπ＋\f(5π,6)))(k∈Z)．


同理可求函数y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3)))的单调递减区间为eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ＋\f(5π,6)，2kπ＋\f(11,6)π))(k∈Z)．


延伸探究


求函数y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)－x))的单调递减区间．


解 y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)－x))＝－2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4)))，


令z＝x－eq \f(π,4)，而函数y＝－2sin z的单调递减区间是eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)＋2kπ，\f(π,2)＋2kπ))(k∈Z)．


∴原函数递减时，得－eq \f(π,2)＋2kπ≤x－eq \f(π,4)≤eq \f(π,2)＋2kπ(k∈Z)，


得－eq \f(π,4)＋2kπ≤x≤eq \f(3π,4)＋2kπ(k∈Z)．


∴原函数的单调递减区间是eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,4)＋2kπ，\f(3π,4)＋2kπ))(k∈Z)．





反思感悟 求正、余弦函数的单调区间的策略


(1)结合正、余弦函数的图象，熟记它们的单调区间．


(2)在求形如y＝Asin(ωx＋φ)(A>0，ω>0)的函数的单调区间时，应采用“换元法”整体代换，将“ωx＋φ”看作一个整体“z”，即通过求y＝Asin z的单调区间而求出原函数的单调区间．求形如y＝Acs(ωx＋φ)(A>0，ω>0)的函数的单调区间同上．


跟踪训练1 求下列函数的单调递增区间：


(1)y＝cs 2x；(2)y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)－x))，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)，2π)).


解 (1)由2kπ－π≤2x≤2kπ(k∈Z)，


所以kπ－eq \f(π,2)≤x≤kπ(k∈Z)，


所以函数y＝cs 2x的单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\c1(kπ－\f(π,2)，kπ))(k∈Z)．


(2)因为y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)－x))＝－sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,6)))，


所以函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)－x))的单调递增区间就是函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,6)))的单调递减区间，


由2kπ＋eq \f(π,2)≤x－eq \f(π,6)≤2kπ＋eq \f(3π,2)，k∈Z，得


2kπ＋eq \f(2π,3)≤x≤2kπ＋eq \f(5π,3)，k∈Z.


因为x∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)，2π))，


所以所求函数的单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\c1(\f(2π,3)，\f(5π,3))).


二、三角函数值的大小比较


例2 比较下列各组中函数值的大小：


(1)cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(23,5)π))与cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(17,4)π))；


(2)sin 194°与cs 160°.


解 (1)cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(23,5)π))＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(－6π＋\f(7,5)π))＝cs eq \f(7,5)π，


cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(17,4)π))＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(－6π＋\f(7,4)π))＝cs eq \f(7,4)π，


∵π

即cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(23,5)π))

(2)sin 194°＝sin(180°＋14°)＝－sin 14°，


cs 160°＝cs(180°－20°)＝－cs 20°＝－sin 70°.


∵0°<14°<70°<90°，∴sin 14°

∴sin 194°>cs 160°.


反思感悟 比较三角函数值大小的步骤


(1)异名函数化为同名函数；


(2)利用诱导公式把角转化到同一单调区间上；


(3)利用函数的单调性比较大小．


跟踪训练2 比较大小：(1)cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(7π,8)))与cs eq \f(7π,6)；


(2)sin eq \f(7,4)与cs eq \f(5,3).


解 (1)cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(7π,8)))＝cs eq \f(7π,8)＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(π－\f(π,8)))＝－cs eq \f(π,8)，


而cs eq \f(7π,6)＝－cs eq \f(π,6)，


∵0cs eq \f(π,6).


∴－cs eq \f(π,8)<－cs eq \f(π,6)，∴cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(7π,8)))

(2)∵cs eq \f(5,3)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋\f(5,3)))，


eq \f(π,2)

又y＝sin x在eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)，\f(3π,2)))上是减函数，


∴sin eq \f(7,4)>sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋\f(5,3)))＝cs eq \f(5,3)，即sin eq \f(7,4)>cs eq \f(5,3).


三、正弦、余弦函数的最值(值域)


例3 求下列函数的值域：


(1)y＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,6)))，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))；


(2)y＝cs2x－4cs x＋5.


解 (1)由y＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,6)))，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))可得x＋eq \f(π,6)∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(2π,3)))，


因为函数y＝cs x在区间eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(2π,3)))上单调递减，所以函数的值域为eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(1,2)，\f(\r(3),2))).


(2)y＝cs2x－4cs x＋5，令t＝cs x，则－1≤t≤1.


y＝t2－4t＋5＝(t－2)2＋1，


当t＝－1，函数取得最大值10；


t＝1时，函数取得最小值2，所以函数的值域为[2,10]．


反思感悟 求三角函数值域的常用方法


(1)求解形如y＝asin x＋b(或y＝acs x＋b)的函数的最值或值域问题时，利用正、余弦函数的有界性(－1≤sin x≤1，－1≤cs x≤1)求解．求三角函数取最值时相应自变量x的集合时，要注意考虑三角函数的周期性．


(2)求解形如y＝asin2x＋bsin x＋c(或y＝acs2x＋bcs x＋c)，x∈D的函数的值域或最值时，通过换元，令t＝sin x(或cs x)，将原函数转化为关于t的二次函数，利用配方法求值域或最值即可．求解过程中要注意t＝sin x(或cs x)的有界性．


跟踪训练3 (1)函数y＝2cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,6)，\f(π,4)))的值域为________．


(2)函数f(x)＝2sin2x＋2sin x－eq \f(1,2)，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(5π,6)))的值域为________．


答案 (1)[－1,2] (2)eq \b\lc\[\rc\](\a\vs4\al\c1(1，\f(7,2)))


解析 (1)∵x∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,6)，\f(π,4)))，


∴2x＋eq \f(π,6)∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,6)，\f(2π,3)))，


∴cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(1,2)，1))，


∴函数的值域为[－1,2]．


(2)令t＝sin x，


∵x∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(5π,6)))，∴eq \f(1,2)≤sin x≤1，


即eq \f(1,2)≤t≤1.


∴f(t)＝2t2＋2t－eq \f(1,2)＝2eq \b\lc\(\rc\)(\a\vs4\al\c1(t＋\f(1,2)))2－1，t∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(1,2)，1))，且该函数在eq \b\lc\[\rc\](\a\vs4\al\c1(\f(1,2)，1))上单调递增．


∴f(t)的最小值为f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))＝1，最大值为f(1)＝eq \f(7,2).


即函数f(x)的值域为eq \b\lc\[\rc\](\a\vs4\al\c1(1，\f(7,2))).





正弦、余弦函数的对称性


典例 函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))的图象的对称轴方程是________，对称中心的坐标是________．


答案 x＝eq \f(k,2)π＋eq \f(π,12)(k∈Z) eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(k,2)π－\f(π,6)，0))(k∈Z)


解析 根据正弦函数的周期性知，过函数图象的最高点或最低点且与x轴垂直的直线均是对称轴，而图象与x轴的交点均为对称中心．


要使sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))＝±1，必有2x＋eq \f(π,3)＝kπ＋eq \f(π,2)(k∈Z)，所以x＝eq \f(k,2)π＋eq \f(π,12)(k∈Z)，


即对称轴方程为x＝eq \f(k,2)π＋eq \f(π,12)(k∈Z)，


而函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))的图象与x轴的交点即为对称中心，


所以令y＝0，即sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))＝0，


所以2x＋eq \f(π,3)＝kπ(k∈Z)，即x＝eq \f(k,2)π－eq \f(π,6)(k∈Z)，


故函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))的图象的对称中心的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(k,2)π－\f(π,6)，0))(k∈Z)．


[素养提升] 正弦曲线、余弦曲线的对称轴一定分别过正弦曲线、余弦曲线的最高点或最低点，即此时的正弦值、余弦值取最大值或最小值；正弦曲线、余弦曲线的对称中心一定是正弦曲线、余弦曲线与x轴的交点，即此时的正弦值、余弦值为0.





1．函数y＝－cs x在区间eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，\f(π,2)))上是( )


A．增函数 B．减函数


C．先减后增函数 D．先增后减函数


答案 C


解析 因为y＝cs x在区间eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，\f(π,2)))上先增后减，


所以y＝－cs x在区间eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，\f(π,2)))上先减后增．


2．正弦函数y＝sin x，x∈R的图象的一条对称轴是( )


A．y轴 B．x轴


C．直线x＝eq \f(π,2) D．直线x＝π


答案 C


解析 当x＝eq \f(π,2)时，y取最大值，∴x＝eq \f(π,2)是一条对称轴．


3．y＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4)))在[0，π]上的单调递减区间为( )


A.eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,4)，\f(3π,4))) B.eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,4)))


C.eq \b\lc\[\rc\](\a\vs4\al\c1(\f(3π,4)，π)) D.eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,4)，π))


答案 D


4．下列关系式中正确的是( )


A．sin 11°

B．sin 168°

C．sin 11°

D．sin 168°

考点 正弦函数、余弦函数的单调性


题点 正弦函数、余弦函数单调性的应用


答案 C


解析 ∵sin 168°＝sin(180°－12°)＝sin 12°，


cs 10°＝sin(90°－10°)＝sin 80°.


∴由正弦函数的单调性，得sin 11°

即sin 11°

5．函数y＝3cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)x－\f(π,4)))在x＝________时，y取最大值．


答案 4kπ＋eq \f(π,2)(k∈Z)


解析 当函数取最大值时，eq \f(1,2)x－eq \f(π,4)＝2kπ(k∈Z)，x＝4kπ＋eq \f(π,2)(k∈Z)．





1．知识清单：


(1)正弦、余弦函数的最大(小)值；


(2)正弦、余弦函数的单调性；


(3)正弦、余弦函数的对称性；


(4)比较大小．


2．方法归纳：整体思想，换元思想．


3．常见误区：单调区间漏写k∈Z；求值域时忽视sin x，cs x本身具有的范围限制．








1．函数f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,6)))的一个单调递减区间是( )


A.eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，\f(π,2))) B．[－π，0]


C.eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(2,3)π，\f(2,3)π)) D.eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)，\f(2,3)π))


答案 D


2．下列不等式中成立的是( )


A．sineq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,8)))>sineq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,10)))


B．sin 3>sin 2


C．sin eq \f(7,5)π>sineq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(2,5)π))


D．sin 2>cs 1


答案 D


解析 ∵sin 2＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－2))＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(2－\f(π,2)))，


且0<2－eq \f(π,2)<1<π，∴cseq \b\lc\(\rc\)(\a\vs4\al\c1(2－\f(π,2)))>cs 1，


即sin 2>cs 1.故选D.


3．当－eq \f(π,2)≤x≤eq \f(π,2)时，函数f(x)＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,3)))有( )


A．最大值1，最小值－1


B．最大值1，最小值－eq \f(1,2)


C．最大值2，最小值－2


D．最大值2，最小值－1


考点 正弦函数、余弦函数的最大值与最小值


题点 正弦函数的最大值与最小值


答案 D


解析 因为－eq \f(π,2)≤x≤eq \f(π,2)，所以－eq \f(π,6)≤x＋eq \f(π,3)≤eq \f(5π,6)，


所以－eq \f(1,2)≤sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,3)))≤1，所以－1≤f(x)≤2.


4．函数y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋\f(π,4)))(ω>0)的周期为π，则其单调递增区间为( )


A.eq \b\lc\[\rc\](\a\vs4\al\c1(kπ－\f(3π,4)，kπ＋\f(π,4)))(k∈Z)


B.eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ－\f(3π,4)，2kπ＋\f(π,4)))(k∈Z)


C.eq \b\lc\[\rc\](\a\vs4\al\c1(kπ－\f(3π,8)，kπ＋\f(π,8)))(k∈Z)


D.eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ－\f(3π,8)，2kπ＋\f(π,8)))(k∈Z)


答案 C


解析 周期T＝π，∴eq \f(2π,ω)＝π，∴ω＝2.


∴y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,4))).


由－eq \f(π,2)＋2kπ≤2x＋eq \f(π,4)≤2kπ＋eq \f(π,2)，k∈Z，


得kπ－eq \f(3,8)π≤x≤kπ＋eq \f(π,8)，k∈Z.


5．已知函数f(x)＝sin(2x＋φ)的图象关于直线x＝eq \f(π,8)对称，则φ可能是( )


A.eq \f(π,2) B．－eq \f(π,4) C.eq \f(3π,4) D.eq \f(π,4)


答案 D


解析 由题意，当x＝eq \f(π,8)时，


f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2×\f(π,8)＋φ))＝±1，


故eq \f(π,4)＋φ＝kπ＋eq \f(π,2)(k∈Z)，


解得φ＝kπ＋eq \f(π,4)(k∈Z)．


当k＝0时，φ＝eq \f(π,4)，故φ可能是eq \f(π,4).


6．sin 470°________cs 760°(填“>”“<”或“＝”)．


答案 >


解析 sin 470°＝sin 110°＝cs 20°>0，cs 760°＝cs 40°>0且cs 20°>cs 40°，


所以sin 470°>cs 760°.


7．函数y＝sin(x＋π)在eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，π))上的单调递增区间为________．


答案 eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)，π))


解析 因为sin(x＋π)＝－sin x，所以要求y＝sin(x＋π)在eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，π))上的单调递增区间，


即求y＝sin x在eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，π))上的单调递减区间，易知为eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)，π)).


8．函数y＝eq \f(1,3)sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－x))(x∈[0，π])的单调递增区间为________．


答案 eq \b\lc\[\rc\](\a\vs4\al\c1(\f(5π,6)，π))


解析 y＝－eq \f(1,3)sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3)))，


∵x∈[0，π]，


∴－eq \f(π,3)≤x－eq \f(π,3)≤eq \f(2π,3).


要求函数的单调递增区间，


则eq \f(π,2)≤x－eq \f(π,3)≤eq \f(2π,3)，


即eq \f(5π,6)≤x≤π.


∴y＝eq \f(1,3)sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－x))(x∈[0，π])的单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\c1(\f(5π,6)，π)).


9．已知函数f(x)＝2cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－2x)).


(1)若f(x)＝1，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,6)，\f(π,4)))，求x的值；


(2)求f(x)的单调递增区间．


解 (1)根据题意cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－2x))＝eq \f(1,2)，


因为eq \f(π,3)－2x＝2kπ±eq \f(π,3)(k∈Z)，


而x∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,6)，\f(π,4)))，故x＝0.


(2)f(x)＝2cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,3)))，


令－π＋2kπ≤2x－eq \f(π,3)≤2kπ，k∈Z，


解得－eq \f(π,3)＋kπ≤x≤kπ＋eq \f(π,6)，k∈Z，


从而f(x)的单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\c1(kπ－\f(π,3)，kπ＋\f(π,6)))(k∈Z)．


10．已知函数f(x)＝2cseq \b\lc\(\rc\)(\a\vs4\al\c1(3x＋\f(π,4))).


(1)求f(x)的单调递增区间．


(2)求f(x)的最小值及取得最小值时相应的x值．


解 (1)令2kπ－π≤3x＋eq \f(π,4)≤2kπ(k∈Z)，


解得eq \f(2kπ,3)－eq \f(5π,12)≤x≤eq \f(2kπ,3)－eq \f(π,12)(k∈Z)．


∴f(x)的单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\c1(\f(2kπ,3)－\f(5π,12)，\f(2kπ,3)－\f(π,12)))(k∈Z)．


(2)当3x＋eq \f(π,4)＝2kπ－π(k∈Z)时，f(x)取最小值－2.


即x＝eq \f(2kπ,3)－eq \f(5π,12)(k∈Z)时，f(x)取最小值－2.











11．函数y＝3cs2x－4cs x＋1，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,3)，\f(2π,3)))的最小值是( )


A．－eq \f(1,3) B.eq \f(15,4) C．0 D．－eq \f(1,4)


答案 D


解析 令t＝cs x，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,3)，\f(2π,3)))，


∴t∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(1,2)，\f(1,2)))，


y＝3t2－4t＋1＝3eq \b\lc\(\rc\)(\a\vs4\al\c1(t－\f(2,3)))2－eq \f(1,3).


∵y＝3eq \b\lc\(\rc\)(\a\vs4\al\c1(t－\f(2,3)))2－eq \f(1,3)在t∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(1,2)，\f(1,2)))上单调递减，


∴当t＝eq \f(1,2)，即x＝eq \f(π,3)时，ymin＝3×eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))2－4×eq \f(1,2)＋1＝－eq \f(1,4).


12．已知ω>0，函数f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋\f(π,4)))在eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，π))上单调递减，则ω的取值范围是( )


A.eq \b\lc\[\rc\](\a\vs4\al\c1(\f(1,2)，\f(5,4))) B.eq \b\lc\[\rc\](\a\vs4\al\c1(\f(1,2)，\f(3,4))) C.eq \b\lc\(\rc\](\a\vs4\al\c1(0，\f(1,2))) D．(0,2]


答案 A


解析 取ω＝eq \f(5,4)，f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5,4)x＋\f(π,4)))，


其减区间为eq \b\lc\[\rc\](\a\vs4\al\c1(\f(8,5)kπ＋\f(π,5)，\f(8,5)kπ＋π))，k∈Z，


显然eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，π))⊆eq \b\lc\[\rc\](\a\vs4\al\c1(\f(8,5)kπ＋\f(π,5)，\f(8,5)kπ＋π))，k∈Z，排除B，C.


取ω＝2，f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,4)))，


其减区间为eq \b\lc\[\rc\](\a\vs4\al\c1(kπ＋\f(π,8)，kπ＋\f(5,8)π))，k∈Z，


显然eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，π))⊈eq \b\lc\[\rc\](\a\vs4\al\c1(kπ＋\f(π,8)，kπ＋\f(5,8)π))，k∈Z，排除D.


13．函数y＝sin x的定义域为[a，b]，值域为eq \b\lc\[\rc\](\a\vs4\al\c1(－1，\f(1,2)))，则b－a的最大值与最小值之和为____．


答案 2π


解析 由图可知，





b－a的最大值为eq \f(13π,6)－eq \f(5π,6)＝eq \f(4π,3)，


b－a的最小值为eq \f(3π,2)－eq \f(5π,6)＝eq \f(2π,3).


所以最大值与最小值之和为eq \f(4π,3)＋eq \f(2π,3)＝2π.


14．函数y＝sin2x＋sin x－1的最大值为________ ，最小值为________．


答案 1 －eq \f(5,4)


解析 令t＝sin x∈[－1,1]，y＝t2＋t－1＝eq \b\lc\(\rc\)(\a\vs4\al\c1(t＋\f(1,2)))2－eq \f(5,4)(－1≤t≤1)，


显然－eq \f(5,4)≤y≤1.





15．若函数f(x)＝sin(2x＋φ)eq \b\lc\(\rc\)(\a\vs4\al\c1(|φ|<\f(π,2)))与函数g(x)＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(ωx－\f(π,6)))(ω>0)的图象具有相同的对称中心，则φ＝________.


答案 eq \f(π,3)


解析 ∵两函数图象具有相同的对称中心，


∴它们的周期相同，


∴ω＝2.令2x＋φ＝kπ(k∈Z)，


则x＝eq \f(kπ,2)－eq \f(φ,2)(k∈Z)，


即f(x)的图象的对称中心为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(kπ,2)－\f(φ,2)，0))(k∈Z)．


令2x－eq \f(π,6)＝k′π＋eq \f(π,2)(k′∈Z)，


则x＝eq \f(k′π,2)＋eq \f(π,3)(k′∈Z)，


即g(x)的图象的对称中心为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(k′π,2)＋\f(π,3)，0))(k′∈Z)．


又g(x)，f(x)的图象的对称中心相同，


则eq \f(kπ,2)－eq \f(φ,2)＝eq \f(k′π,2)＋eq \f(π,3)(k，k′∈Z)，


即φ＝(k－k′)π－eq \f(2π,3)(k，k′∈Z)，


又∵|φ|

∴φ＝eq \f(π,3).


16．已知ω是正数，函数f(x)＝2sin ωx在区间eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,3)，\f(π,4)))上是增函数，求ω的取值范围．


解 由－eq \f(π,2)＋2kπ≤ωx≤eq \f(π,2)＋2kπ(k∈Z)，ω>0，得－eq \f(π,2ω)＋eq \f(2kπ,ω)≤x≤eq \f(π,2ω)＋eq \f(2kπ,ω)，


∴f(x)的单调递增区间是eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2ω)＋\f(2kπ,ω)，\f(π,2ω)＋\f(2kπ,ω)))，k∈Z.


根据题意，得eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,3)，\f(π,4)))⊆eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2ω)＋\f(2kπ,ω)，\f(π,2ω)＋\f(2kπ,ω)))(k∈Z)，


从而有eq \b\lc\{\rc\ (\a\vs4\al\c1(－\f(π,2ω)≤－\f(π,3)，,\f(π,2ω)≥\f(π,4)，,ω>0))解得0<ω≤eq \f(3,2).


故ω的取值范围是eq \b\lc\(\rc\](\a\vs4\al\c1(0，\f(3,2))).正弦函数
余弦函数
图象
定义域
R
R
值域
[－1,1]
[－1,1]
单调性
在eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ－\f(π,2)，2kπ＋\f(π,2)))(k∈Z)上单调递增，


在eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ＋\f(π,2)，2kπ＋\f(3,2)π))(k∈Z)上单调递减
在[2kπ－π，2kπ](k∈Z)上单调递增，


在[2kπ，2kπ＋π](k∈Z)上单调递减
最值
x＝eq \f(π,2)＋2kπ(k∈Z)时，ymax＝1；


x＝－eq \f(π,2)＋2kπ(k∈Z)时，ymin＝－1
x＝2kπ(k∈Z)时，ymax＝1；


x＝2kπ＋π(k∈Z)时，ymin＝－1