









15.2021届高考数学(文)大一轮复习(课件 教师用书 课时分层训练)_热点探究课6 概率与统计中的高考热点问题 (3份打包)
展开热点二
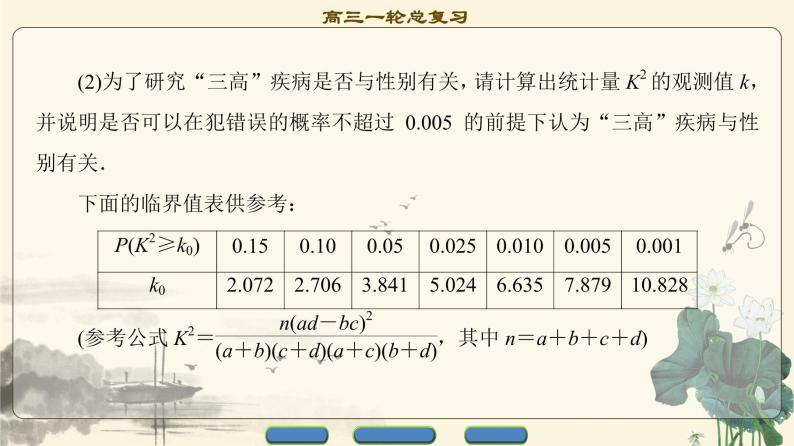
热点三
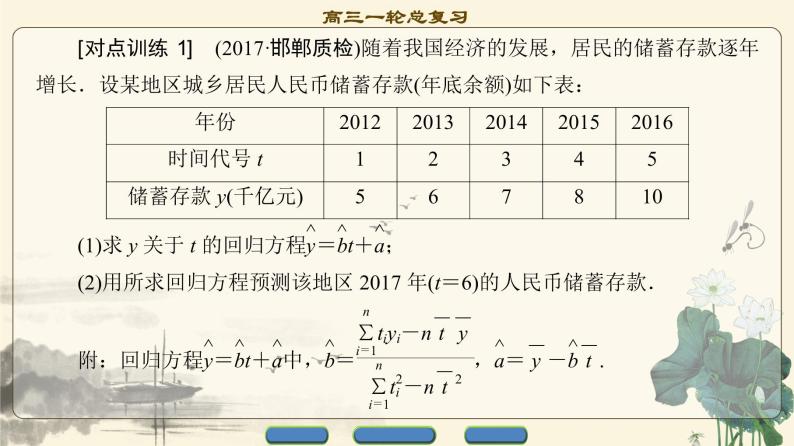
热点探究训练
热点探究训练(六)点击图标进入…














您所在的“深圳市第一中学”云校通为试用账号,试用账号每位老师每日最多可下载 10 份资料 (今日还可下载 0 份),请取消部分资料后重试或选择从个人账户扣费下载。
您所在的“深深圳市第一中学”云校通为试用账号,试用账号每位老师每日最多可下载10份资料,您的当日额度已用完,请明天再来,或选择从个人账户扣费下载。
您所在的“深圳市第一中学”云校通余额已不足,请提醒校管理员续费或选择从个人账户扣费下载。
正在打包资料,请稍候…
预计需要约10秒钟,请勿关闭页面
服务器繁忙,打包失败
请联系右侧的在线客服解决
单次下载文件已超2GB,请分批下载
请单份下载或分批下载
支付后60天内可免费重复下载

注册成功
下载需要:0 张下载券
账户可用:0 张下载券
如何免费获得下载券?
加入教习网教师福利群,群内会不定期免费赠送下载券及各种教学资源, 立即入群